Determination of elastic moduli of concrete by Impulse Excitation Technique
This website section goals are to present the theory and methodology for non-destructive determination of the dynamic elasticity modulus of concrete (Ed) by Impulse Excitation Technique [1], a resonance frequencies method [2], for the estimation of the chord modulus of elasticity (Ec) from Ed.
Introduction
Elastic moduli are fundamental properties and, increasingly, designers specify minimum values to be met due to the evolution of the concrete compressive strength. However, these properties are not often measured, instead, they are frequently estimated from the compressive strength with considerable uncertainty. The methods based on resonance frequencies [2], in particular the Impulse Excitation Technique (IET) [1], are more accurate, practical and accessible than static methods for elastic moduli determination. Additionally, they allow the non-destructive measurement of these properties in the same specimens to be tested for compressive strength.
Concrete is a composite material, in which aggregate particles or fragments are bonded by a matrix [3]. When the matrix or the aggregates are loaded individually, both present a linear stress-strain curve and the modulus of elasticity determination is straightforward. However, concrete does not present such linearity due to the presence and development of cracks and microcracks at the interface between the matrix and the aggregates [3,4].
Concretes can be classified according to their characteristic axial compressive strength (fck): those with fck up to 20 MPa are named low strength concretes, with fck between 20 MPa and 40 MPa, medium strength concretes, and with fck greater than 40 MPa, high strength concretes [3]. Figure 1 shows an example of high strength concrete application, the Leopoldo 1201 building. Built in São Paulo (Brazil), this building applied concrete with a chord modulus of elasticity of 48 GPa developed by PhD Engenharia, Engemix and Nortis.
![Figure 1 - Leopoldo 1201 building construction, which used concrete with a modulus of elasticity of 48 GPa (2021) [8].](/images/F1-EN-Leopoldo-building-concrete-record-modulus.jpg)
Figure 1 - Leopoldo 1201 building construction, which used concrete with a modulus of elasticity of 48 GPa (2021) [8].
It is usual to estimate the concrete chord modulus of elasticity from the axial compressive strength using empirical models [3,4]. However, there are two important sources of uncertainty that must be taken into account: the first one is the model employed validity and limitations [3,4], which depends on the concrete classification, the second one is the high dispersion of compressive strength test results. A practical, accurate and low-cost alternative is the estimation of Ec from the dynamic elasticity modulus (Ed) using the Popovics model [2,5-7]. To determine the Ed, the Impulse Excitation Technique (IET) can be used [1,2]. IET is based on the specimen resonance frequencies and, unlike static tests, takes just a few minutes, has low uncertainty and high reproducibility [1,2]. In this case, both properties (Ec and Ed) are related only to the elastic characteristics of the material and the starting point is accurate and measurable non-destructively [2,6,7]. Figure 2 shows a concrete application with defined chord modulus of elasticity for slender structures and large spans [9].
![Figure 2 - Application of concrete with defined and dimensioned chord modulus of elasticity for slender structures and large spans [9].](/images/F2-EN-Concrete-defined-chord-modulus-slender-span.png)
Figure 2 - Application of concrete with defined and dimensioned chord modulus of elasticity for slender structures and large spans [9].
When compared to methods based on the speed of ultrasonic waves, the Impulse Excitation Technique presents significant advantages for the concrete elastic modulus determination, for example, it is not necessary to couple transducers to the specimen and the results are less sensitive to the operator skill and Poisson's ratio estimation [7]. Additionally, the Impulse Excitation Technique allows the damping simultaneous determination, does not require constant calibration and is less influenced by the aggregates size.
Civil construction is the main consumer of concrete and it is highly competitive and dynamic. Technological advances that improve and facilitate the concrete technological control are highly welcome for designers, builders, concrete service companies and laboratories.
Moduli of elasticity of concrete
In general, the modulus of elasticity, or Young’s modulus, consists in the coefficient between stress and strain during the material elastic regime. However, the stress-strain curve of concrete is non-linear and the slope varies with stress and curve fitting method. The denomination also depends on the load application regime, which can be static or dynamic. Figure 3 illustrates the typical stress-strain curves of concrete specimen and its components [3]. Although the aggregate and the matrix present linear behavior, the concrete presents a non-linear behavior due to the presence of cracks on the interface between the matrix and aggregates

Figure 3 - Typical behavior of the stress-strain curve for concrete and its main components [3].
The standards describe distinct methodologies and there is no general consensus on the best way to define, calculate, predict and test the modulus of elasticity of concrete [7]. Based on static tests, it is possible to obtain chord modulus of elasticity, that varies according to the points considered of the stress-strain curve (Fig. 4). In addition, other aspects such as experimental parameters and the specimen size affect this property determination [3,4].
![Figure 4 - Different approaches to determine the modulus of elasticity from the stress-strain curve [10].](/images/F4-EN-Approach-determine-modulus-elasticity-concrete.jpg)
Figure 4 - Different approaches to determine the modulus of elasticity from the stress-strain curve [10].
The modulus of elasticity of concrete may be also obtained by non-destructive tests, usually based on the natural frequencies of vibration or on the propagation velocity of ultrasonic waves (modulus of elasticity obtained by these means are called dynamic) [7,10]. The employment of non-destructive tests has relevant advantages, such as the possibility of submitting the same specimen to other tests and follow curing or degradation processes. In this way, the uncertainty of the results and the total amount of specimens needed for the same study are reduced.
Opposed to many mechanical static tests, dynamic tests submit the material to low stress levels, so there is minimum probability of appearing effects related to the creep and nucleation of micro-cracks on the material.
The dynamic modulus is usually 20% greater than static moduli for high-strength concretes, 30% for medium-strength concretes, and 40% for low-strength concretes [3].
Parameters affecting the modulus of elasticity of concretes
The elastic properties of concrete depend largely on the properties of its components and of the interface between the matrix and the aggregates. Additionally, there are external factors that can influence the elasticity modulus, for example, the specimen moisture content. Figure 5 shown the main parameters that affect the modulus of elasticity of concrete.
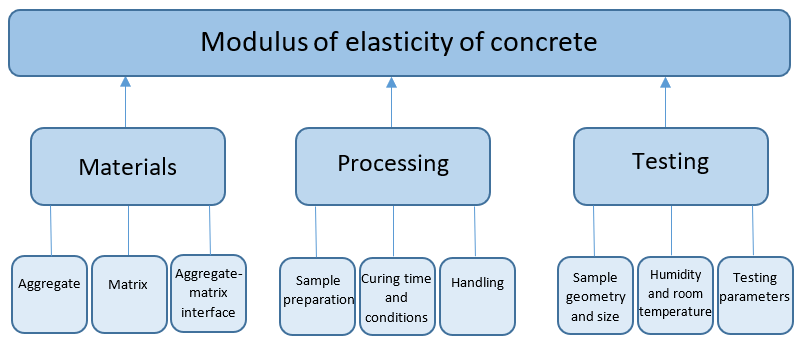
Figure 5 - Parameters influencing the modulus of elasticity of concrete.
• Aggregate
The aggregate modulus of elasticity is generally greater than of the cement paste (matrix), being porosity one of the main variables. The higher the porosity of an aggregate, the lower its modulus of elasticity and of the concrete in which it was used (Fig. 6) [3]. For example, high-density (low porosity) aggregates such as granite, basalt and volcanic rocks have a higher modulus of elasticity than low-density (porous) aggregates such as sandstones, limestones, and gravels.
Aggregates porosity variation affects the modulus of elasticity of concrete; however, it does not significantly affect the compressive strength, mainly for low- and medium-strength concretes. This fact demonstrates one of the examples in which the influence of a variable is not the same for the mechanical strength and modulus of elasticity, explaining the difficulty in finding a general model to correlate modulus of elasticity to compressive strength [3].
![Figure 6 - Influence of the aggregate porosity on the modulus of elasticity of concrete (adapted graph [11]).](/images/F6-EN-Influence-aggregate-porosity-moduluselasticity-concrete.jpg)
Figure 6 - Influence of the aggregate porosity on the modulus of elasticity of concrete (adapted graph [11]).
Aggregates shape, average size, superficial texture and mineralogical composition affect the modulus of elasticity of concrete. These aspects have an effect on the interface between the matrix and the aggregates, determining this region tendency to crack [3,4]. Besides, the aggregate volume fraction in the mixture will also affect the modulus of elasticity.
• Matrix
As well as the aggregates, the cement paste porosity is related to its modulus of elasticity, which in turn, will influence the concrete properties. The parameters affecting the matrix final porosity are diverse, being the main ones the water-cement ratio (Fig. 7), the entrapped air content, the mineral additions, and the cement hydration.
![Figure 7 - Effect of the water-cement ratio on the modulus of elasticity (adapted graph [12]).](/images/F7-EN-Effect-water-cement-ratio-modulus-elasticity-concrete.jpg)
Figure 7 - Effect of the water-cement ratio on the modulus of elasticity (adapted graph [12]).
The hydration of the cement phases during the curing process affects the matrix final porosity, and the main voids found in this region are due to the spaces not occupied by the hydration reaction products and also to the presence of entrapped air.
• Processing
Processing a concrete specimen involves a mixture of correct quantity of raw material, modeling, curing, extracting from the molds, and the final finishing of the specimens (capping and grinding). During the preparation, the curing process must be controlled (Fig. 8 illustrates the influence of the curing temperature on the modulus of elasticity) and it must be guaranteed that there is no segregation of the components. Caring for the specimen’s storage and transportation are also important because the lack of control of these variables may compromise the results.
![Figure 8 - Modulus of elasticity as a function of the age and curing temperature (adapted graph [13]).](/images/F8-EN-Modulus-elasticity-age-curing-temperature.jpg)
Figure 8 - Modulus of elasticity as a function of the age and curing temperature (adapted graph [13]).
• Testing
The specimen conditions must be evaluated before testing, since its properties can be affected by environmental variables. For example, the modulus of elasticity in wet conditions can be about 15% higher than in dry conditions [3]. For static tests, an important variable is the loading speed, intermediate speeds must be used. For very low speeds, the phenomenon of concrete creep will decrease the modulus of elasticity, on the other hand, high velocities can lead to overestimated results [14].
According to ABNT NBR 8522-1&2:2021 standard [2], specimens for modulus of elasticity testing should be cylinders with a 2:1 height to diameter ratio. It is important to mention that similar standards specify other geometries. However, it is not advisable to compare results obtained with specimens of different geometries or dimensions [2-4,7].
Methodologies to determine the modulus of elasticity of concrete
• Static tests
ABNT NBR 8522-1&2:2021 [15] standard and related ones describe two static and one dynamic methodologies for determining the concrete modulus of elastic, and states the use of cylindrical specimens prepared with a ratio of 2:1 (height to diameter).
The first static methodology describes obtaining the secant modulus (Ecs), defined as the slope of the secant line to the stress-strain curve passing two points on the graph, where the first corresponds to a stress of 0.5 MPa and the second at the desired stress. The secant modulus (Ecs) is equal to the chord modulus (Ec) if the second point is set at 40% of the concrete compression strength. The second methodology describes obtaining the initial tangent deformation modulus (Eci), which is considered equivalent to the secant modulus between a fixed stress (σa = 0.5 MPa) and 30% of the concrete compression strength. For static methods, preload cycles are recommended to accommodate the specimen in the testing machine before recording values (Fig. 9).
![Figure 9 – Pre-loading procedure by ABNT NBR 8522-1&2: [15].](/images/F9-EN-Pre-loading-procedure-elastic-modulus-concrete.png)
Figure 9 – Pre-loading procedure by ABNT NBR 8522-1&2: [15].
It is worth highlighting that there is not a wide consensus on the testing parameters for the modulus of elasticity of concrete determination. Standards present significant differences in parameters which affects the final result, such as the loading rate, number of pre-loadings cycles, maximum stress, geometry and dimensions. Furthermore, the determination of strain at the beginning of the stress-strain curve is difficult due to the presence of imperfections in the specimens’ surfaces and accommodation of the testing machine [16]. Interlaboratory trials have shown the results dispersion around 15% [6,17]. Therefore, it is imperative to provide information about the adopted testing procedure when reporting the modulus of elasticity of concrete.
• Modulus of elasticity estimation by the compressive strength
There are empirical models allowing the estimation of the modulus of elasticity of concrete by the compressive strength. However, these models must be used with caution because compressive strength and modulus of elasticity are distinct mechanical properties and differently influenced by the concrete variables [3,4]. There is no consensus on the best model for predicting the modulus of elasticity by the compressive strength, since there are questionings about national and international standards that apply this approach [6,18-20]. Figure 10 illustrates the results of the main models used for predicting the modulus of elasticity (Young’s modulus) of concretes based on the compressive strength.
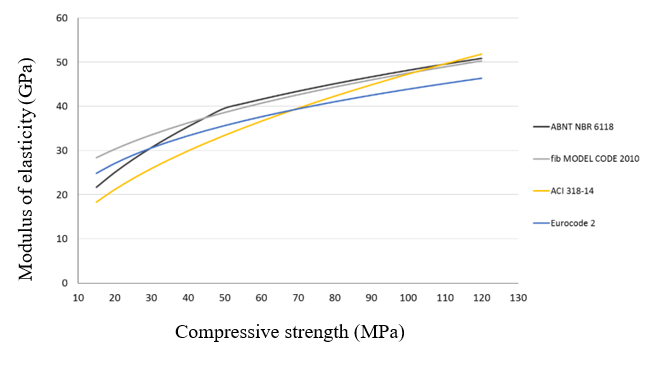
Figure 10 - Available models in standards for predicting the modulus of elasticity from compressive strength value.
The modulus of elasticity of concrete is generally specified in project through a correlation with compressive strength. Because of that, it is not rare for a concrete supplier to be bound to fabricate a material with greater compressive strength than the specified to compensate the uncertainty of the modulus of elasticity estimation, avoiding the risk of having its material refused [19,21].
The main equations correlating compressive strength to the modulus of elasticity of concrete are:
- Brazilian Association of Technical Standards NBR 6118 (ABNT NBR 6118) [22]:
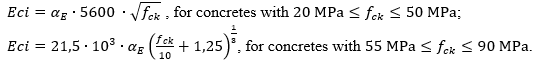
- Fédération internationale du béton -Model Code for Concrete Structures 2010 (fib MODEL CODE 2010) [23]:
For both models, Eci refers to the initial tangent elastic modulus at 28 days, αE is a dimensionless constant that depends on the type of aggregate used for the concrete fabrication (Table 1) and fck is the specific compressive strength of the concrete.
Table 1 – Value of αE according to the type of aggregate used for the concrete fabrication.

- American Concrete Institute – 318: Building code requirements for structural concrete (ACI 318) [24]

Ec is the secant elastic modulus obtained from the start point up to a level of stress equal to 0.45fc, ωc is the concrete density (in kg/m3) and fc is the specified compressive strength.
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures (EUROCODE 2) [25]
Ecm is the secant elastic modulus obtained from the start point up to a level of stress equal to a 0.4fcm and fcm is the average compressive strength.
Methodology for Ed determination and Ec estimation
Dynamic tests and Impulse Excitation Technique
A practical, precise and accurate alternative to obtain the concrete chord modulus of elasticity (Ec) is to estimate it from the dynamic modulus of elasticity (Ed) determined by the specimen resonance frequencies [7]. Additionally, the dynamic modulus of elasticity is especially relevant for applications where the concrete is subjected to dynamic loads, for example, in applications where the structure sudden loading occurs [26]. Because only small stresses are applied during the determination of this property, there is no induction of microcracking, as well as there is no creep effect. For this reason, it can be considered that the dynamic modulus is associated with purely elastic phenomena [4].
The ASTM C215 [2] standard describe the main methodologies for the characterization of the dynamic elastic moduli of concrete specimens. This standard predicts the characterization of the specimen’s natural frequencies of vibration and, along with its mass and dimensions, the calculation of the dynamic elastic modulus. When the specimen excitation is by a short mechanical impulse, this variation is called Impulse Excitation Technique (IET) [1]. IET used has grown in the civil construction sector and is a practical alternative obtain concrete chord modulus of elasticity [6,7,27-30]. Next, the main advantages of employing IET:
- Allows the reduction of the number of specimens and to intercalate the test with other processes for being non-destructive;
- Provides more precise results than static tests because of the lower quantity of variables and less susceptibility to experimental errors [27,30];
- Speeds up the results obtainment since the characterization takes only few minutes and may be repeated as many times as needed;
- Allows following the modulus of elasticity of a specimen in dependence of time (for example, to follow the curing process; Fig. 11);
- Turns it possible to evaluate the progressive damage since the cracking lowers the material’s stiffness and, as a consequence, reduces the natural frequency of vibration [26];
- Turns it possible to monitor the variation of the modulus of elasticity of the same specimen as a function of other variables, such as temperature or the number of thermal cycles (ASTM C666 [31]).
![Figure 11 - Monitoring the dynamic elastic modulus of three specimens in dependence of their age [32].](/images/F11-EN-Dynamic-elasti-modulus-concrete-dependence-age.gif.png)
Figure 11 - Monitoring the dynamic elastic modulus of three specimens in dependence of their age [32].
Correlation between the static and dynamic modulus of elasticity
The difference between the static modulus of elasticity and the dynamic elastic modulus of a concrete specimen is mainly due to the fact that this material possesses a viscoelastic behavior, meaning that its behavior varies according to the strain rate applied during the test (Fig. 12).
![Figure 12 – Curves obtained from theoretical models demonstrating the influence of the strain rate on the stress-strain curves of a concrete [14].](/images/F12-EN-Stress-strain-curves-influence-strain-rate-concrete.png)
Figure 12 – Curves obtained from theoretical models demonstrating the influence of the strain rate on the stress-strain curves of a concrete [14].
The lower the rate applied the longer the time for relaxation and the lower the slope of the stress-strain curve. On the other hand, the higher the rate, the shorter the time for relaxation and the greater the slope of the stress-strain curve (Fig. 12). The strain rate applied during a dynamic test is always higher to the one applied at static tests, as well as the strain levels applied at a dynamic test are lower. Therefore, the dynamic elastic modulus will be always greater than or equal to the modulus obtained from a static test [14,33,34].
Below find the Popovics model for predicting the concrete chord modulus of elasticity (Ec) from the dynamic elastic modulus (Ed) [35]. This model presents good results for low- and medium-density concretes at different ages (between one day and one year), and also at different classes of compressive strength (between 5.4 Mpa and 82.7 Mpa) [6,35].
k is a constant which depends on the units used (k=0.107 when the modulus is expressed in Pa and density in kg/m³) and ρ is the concrete density.
Step by step for the estimation of Ec using IET
The step-by-step procedure for estimating the Ec of a concrete specimen from the Ec module obtained by the Impulse Excitation Technique is presented below.
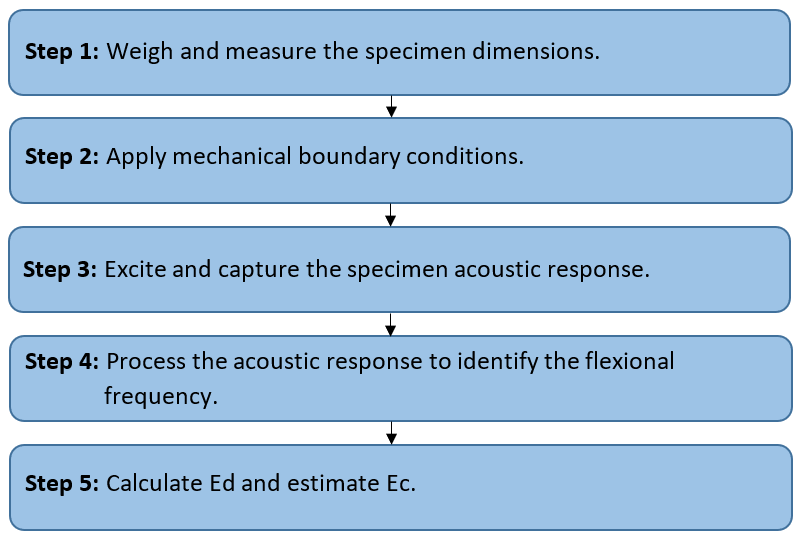
Figure 13 - Flowchart for estimating the Ec using the Impulse Excitation Technique.
Step 1 - Weigh and measure the specimen dimensions:
The first step is to weigh and measure the dimensions of the specimen. Typical specimens are cylinders 200 mm high and 100 mm in diameter. The height must be equal to the average between the maximum and minimum measurement, the diameter must be equal to the average of two orthogonal measurements taken at half height [2].
Step 2 - Apply mechanical boundary conditions:
The second step consists of supporting the specimen at positions equal to 0.224h from the end (h is the height) and positioning the acoustic sensor and the impact device on opposite sides at the center of the specimen with respect to the vibration plane.
Step 3 - Excite and capture the specimen acoustic response:
The third step consists of exciting the specimen with the application of a single impact and capturing the corresponding acoustic response with an acoustic sensor. We recommend using the Sonelastic® System shown in Fig. 14.

Figure 14 - Sonelastic® System for concrete specimens: Computer with Sonelastic® software, signal acquisition module ADAC, CA-DP acoustic sensor, SA-BC support and medium manual impulse device.
Step 4 - Process the acoustic response to identify the flexional frequency:
The fourth step consists of processing the acoustic response to identify the flexional frequency. This processing is carried out automatically by the Sonelastic® Software.
Step 5 - Calculate Ed and estimate Ec:
The fifth and final step consists of calculating the Ec according applying the Popovics model [35]:
The input values correspond to the concrete density (ρ) in kg/m³ and to the dynamic modulus of elasticity (Ed) in MPa. One can also prepare a report specifying the containing all data that may affect the results (material, processing, curing, specimen geometry, age and test conditions).
Detailing the Ed determination by IET
IET fundamentals
The resonance techniques [1,2,15] consists essentially in determining the elastic moduli from the specimen natural frequencies of vibration. When the frequencies are excited by a short mechanical impulse, it is called Impulse Excitation Technique (IET). In the IET, the mechanical impulse is followed by the acoustic response acquisition using an acoustic sensor and proper hardware. Then, a mathematical treatment (Fast Fourier Transform) is performed on the acoustic signal in order to obtain the frequency spectrum and the resonance frequencies. Next, the dynamic elastic modulus is calculated using the standard equations, which also considers the specimen geometry, mass and dimensions.
For the target resonance and vibration mode excitation, it is necessary to set up specific boundary conditions. Figure 15 presents an example of a cylindrical specimen support, excitation position and acoustic response acquisition for the fundamental flexural vibration mode [36].
![Figure 15 - Arrangement for determining the dynamic modulus of elasticity of a cylindrical concrete specimen according to ASTM C215-20 [2] and using a Sonelastic® System.](/images/F15-EN-Specimen-support-dynamic-elastic-modulus-concrete-C215.jpg)
Figure 15 - Arrangement for determining the dynamic modulus of elasticity of a cylindrical concrete specimen according to ASTM C215-20 [2] and using a Sonelastic® System.
Vibration modes
A specimen may vibrate in different ways and for each mode there is a specific fundamental frequency. Figure 16 presents the main fundamental vibration modes of a cylinder and of a disc.
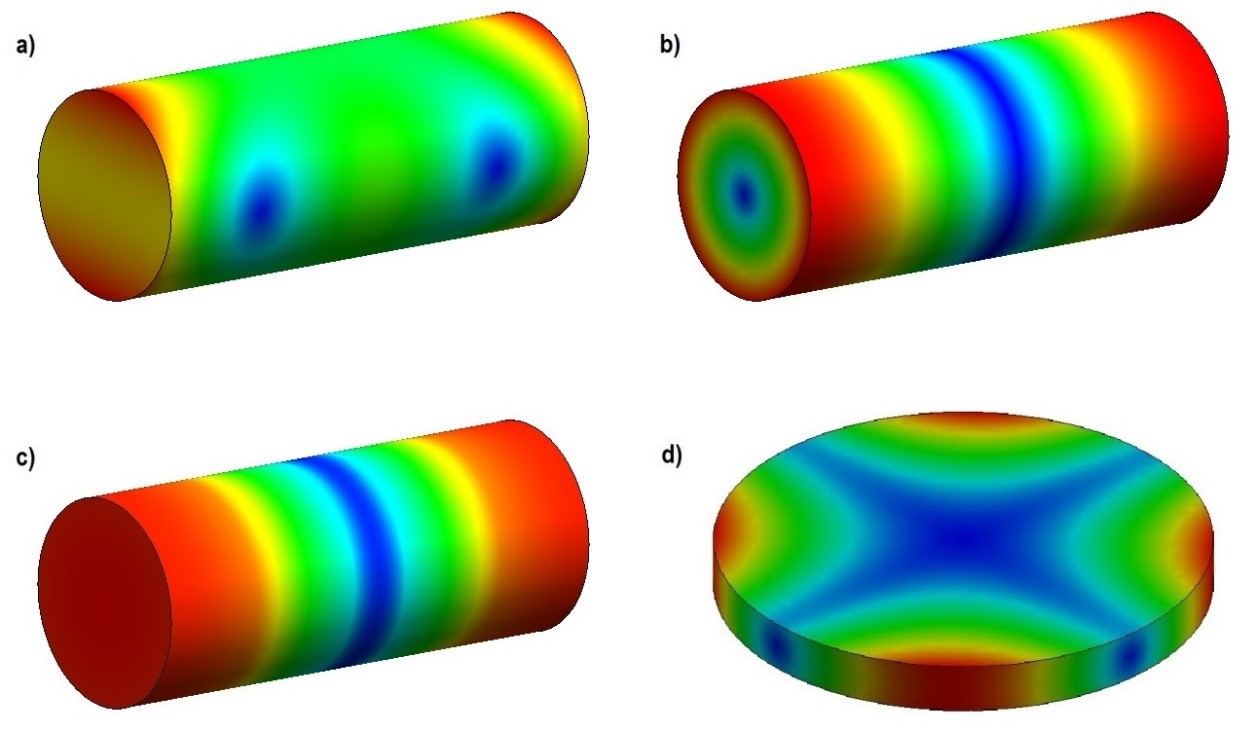
Figure 16 - Fundamental vibration modes: a) Flexural, b) Torsional, c) Longitudinal, and d) Planar. In blue areas the amplitude of vibration is minimum, whereas it is maximum at the red ones.
The boundary conditions imposed during characterization are responsible for determining which vibration mode will be excited. The fundamental frequency of these modes depends on the geometry, mass, dimensions and elastic moduli of the material.
Figures 17a-c present the optimum boundary conditions for the main vibration modes of a cylinder [1]. The dynamic elastic modulus is calculated by employing the equations described by C215 standard [2], which is based on the resonant frequencies of the specimen, its mass and dimensions.
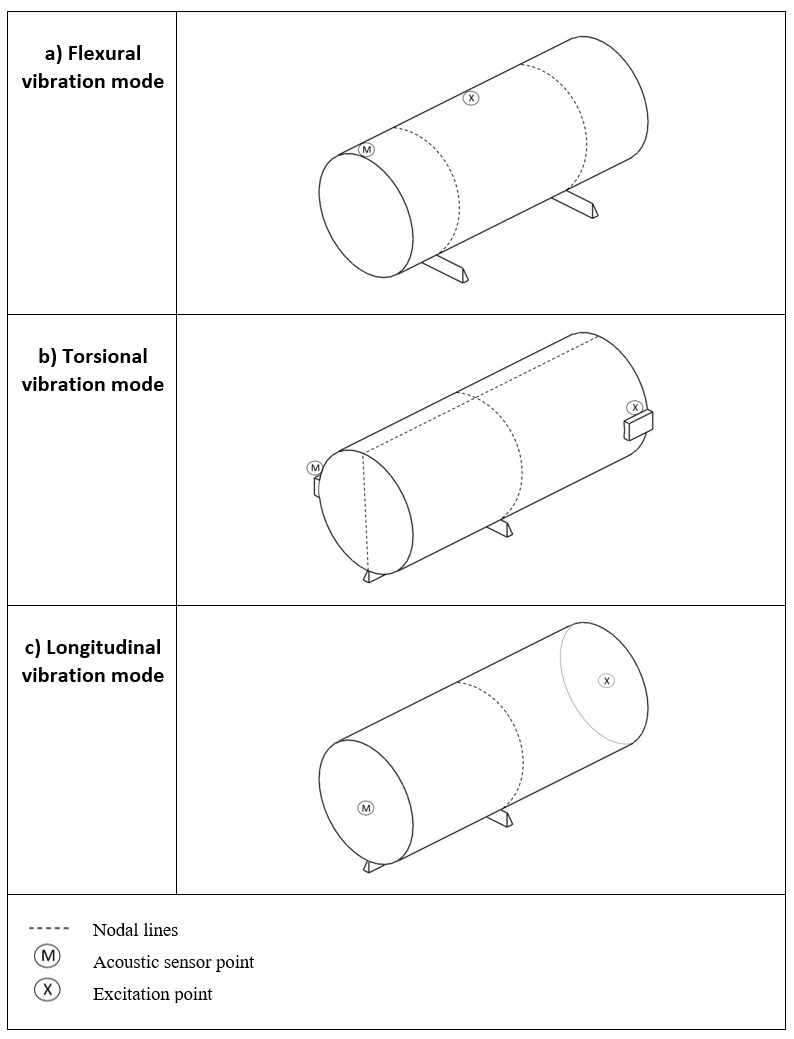
Figure 17 - Boundary conditions set up for the specimen for the excitation of (a) flexural, (b) torsional and (c) longitudinal vibration modes.
Elastic properties and vibration modes
In general, the main elastic properties of a material are the modulus of elasticity (or Young’s modulus), the shear modulus and the Poisson’s ratio. The Impulse Excitation Technique allows the characterization of these properties as detailed next in dependence of the vibration mode.
• Elasticity modulus (Young’s modulus)
- Longitudinal vibration mode: When the specimen is excited in longitudinal mode, the elastic modulus obtained refers to the orientation parallel to the specimen’s length. Therefore, this is dynamic modulus equivalent to the value obtained from a tensile or compressive test.
- Flexural vibration mode: When a specimen is flexed, both tension and compression stresses occur, as shown in Fig. 18 [37]. For homogeneous and isotropic materials, the elastic modulus obtained from a bending test coincides with the elastic modulus measured longitudinally. Therefore, the value of the dynamic elastic modulus obtained through the flexural vibration mode is the same as the one obtained through the longitudinal vibration mode [37]. Nevertheless, it is known that, when flexed, the surface of the material is the region submitted to the greatest tensions. For this reason, if the stiffness of specimen’s surface and its center is different (for example, if there is a stiffness gradient along the thickness), or if the specimen presents some flaws such as pores, cracks and micro-cracks on the surface, there will be a difference between the values obtained through flexural and longitudinal vibration modes. There is a range of publications presenting a comparison between the modulus of elasticity obtained from both the flexural and longitudinal vibration modes [5-7].
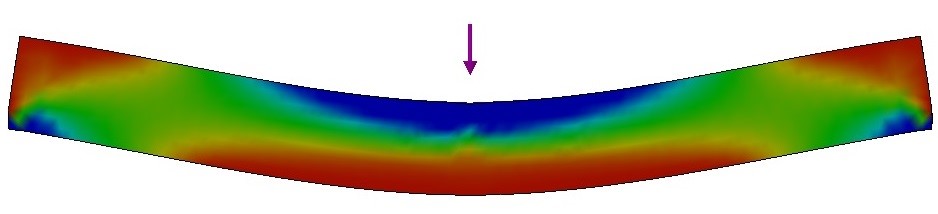
Figure 18 - Tensile (red) and compression (blue) regions of stress during a bending test.
• Shear modulus
- One of the main ways to obtain the shear modulus from a static test is by a torsion test. In the case of the Impulse Excitation Technique, the principle is similar, nonetheless in this case, it is necessary to provide the boundary conditions for the specimen to vibrate under the torsional mode (see Fig. 17b). In the case of the rectangular specimens, it is only need to excite the specimen near one of the lateral edges, outside de nodal lines, and acquire the acoustic response at the symmetrical edge. However, in the case of cylindrical specimens, it is necessary to couple small tabs near the specimen edges in order to excite and detect the torsional mode.
• Poisson’s ratio
The characterization of the Poisson’s ratio by Impulse Excitation Technique occurs indirectly, based on the correlation between the material modulus of elasticity and shear modulus [1], which is given by the following equation:
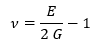
E is the modulus of elasticity, G is the shear modulus and ν is the Poisson’s ratio.
Examples of customers and applications in the area of concrete, cementitious materials and rocks.
Referências bibliográficas
[1] ASTM E1876, Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; designation: E1876-21. ASTM International, 2021.
[2] ASTM C215, Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens; designation: C215-19. ASTM International, 2019.
[3] MEHTA, P. K.; MONTEIRO, P. J. M. Concreto: Microestrutura, Propriedades e Materiais. 3 ed. São Paulo: IBRACON, 2008. 674 p.
[4] NEVILLE, A. M. Properties of Concrete. 5th ed. England: Pearson, 2011.
[5] MALHOTRA, V. M.; SIVASUNDARAM, V. Resonant Frequency Methods. In.: MALHOTRA, V. M.; CARINO, N. J. (Eds.). Handbook on Nondestructive Testing of Concrete. West Conshohocken: CRC Press LLC (ASTM International), 2004. p. 7-1 – 7-21.
[6] POPOVICS, J. S. A Study of Static and Dynamic Modulus of Elasticity of Concrete. University of Illinois, Urbana, IL. ACI-CRC Final Report. 2008.
[7] PACHECO, J.; BILESKY, P.; MORAIS, T. R.; GRANDO, F.; HELENE, P. Considerações sobre o Módulo de Elasticidade do Concreto. In: Congresso Brasileiro do Concreto, 56°, 2014, Natal - RN, Anais, IBRACON.
[8] Disponível em:
[9] Disponível em:
[10] ALMEIDA, S. M. Análise do módulo de elasticidade estático e dinâmico do concreto de cimento Portland através de ensaios de compressão simples e de frequência ressonante. 2012. 213 p. Dissertação (mestrado) – Escola de Engenharia, Universidade Federal de Minas Gerais, Belo Horizonte, 2012.
[11] GUÐMUNDSSON, J. G. Long-term creep and shrinkage in concrete using porous aggregate – the effects of elastic modulus. 2013. 80 p. Thesis (Master of Science) - School of Science and Engineering, Reykjavík University, Iceland, 2013.
[12] HAECKER, C. -J. et al. Modeling the linear elastic properties of Portland cement paste. Disponível em:
[13] KIM, J. K.; HAN, S. H.; SONG, Y. C. Effect of temperature and aging on the mechanical properties of concrete: Part I. Experimental results. Cement and Concrete Research, v. 32, 2002, pp. 1087-1094.
[14] SHKOLNIK, I. E. Influence of high strain rates on stress–strain relationship, strength and elastic modulus of concrete. Cement & Concrete Composites, v. 30, 2008, pp. 1000-1012.
[15] ABNT NBR 5738:2015 Concreto - Procedimento para moldagem e cura de corpos de prova. 2015.
[16] ARAÚJO, S. S. Influência do tipo de medição na determinação do módulo estático de elasticidade do concreto. 2011. 212 p. Dissertação (mestrado) – Escola de Engenharia Civil, Universidade Federal de Goiás, Goiânia, 2011.
[17] AHN, N.; YANG, S. An Experimental study of the effect of temperature and age on the properties of concrete. In: Proceedings of the Eastern Asia Society for Transportation Studies, v. 4, 2003, pp. 408-416.
[18] NETO, A. A. M.; HELENE, P. Módulo de elasticidade: dosagem e avaliação de modelos de previsão do módulo de elasticidade de concretos. In: Congresso Brasileiro do Concreto, 44°, 2002, Belo Horizonte - MG, Anais, IBRACON.
[19] BORIN, L. A.; BAUER, R. J. F.; FIGUEIREDO, A. D. Risco de rejeição de concretos devido à não conformidade com os parâmetros normalizados para o módulo de elasticidade. Construindo, Belo Horizonte, v. 4, No. 2, 2012, pp. 79-89.
[20] ARAÚJO, J. M. O módulo de deformação longitudinal do concreto. Rio Grande: Dunas, 2001. 25 p. (Estruturas de Concreto, Número 3).
[21] DE MARCHI, R. D. Estudo sobre a variabilidade do módulo de deformação do concreto associada a fatores intrínsecos à produção do material. 2011. 121 p. Dissertação (mestrado) – Escola Politécnica, Universidade de São Paulo, São Paulo, 2011.
[22] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 6118: Projeto de estruturas de concreto - Procedimento. Rio de Janeiro: ABNT, 2014. 238 p.
[23] FÉDÉRATION INTERNATIONALE DU BÉTON. fib Model Code for Concrete Structures 2010. Ernst & Sohn, 2013, 434 p.
[24] ACI 318-02 Building code requirements for structural concrete, ACI Manual of Concrete Practice Part 3: Use of Concrete in Buildings – Design, Specifications, and Related Topics, 443 pp.
[25] EUROPEAN COMMITTEE FOR STANDARDIZATION. EUROCODE 2: design of Concrete Structures: part 1-1: general rules and rules for buildings. EN 1992-1-1. Brussels, Belgium, 2004.
[26] ALMEIDA, S. F.; HANAI, J. B. Análise dinâmica experimental da rigidez de elementos de concreto submetidos à danificação progressiva até a ruptura. Cadernos de Engenharia de Estruturas, São Carlos, v. 10, No. 44, 2008, pp. 49-66.
[27] CANESSO, F. A. C.; CORREA, E. C. S; SILVA, A. P. E.; AGUILAR, M. T. P.; CETLIN, P. R. Módulo de elasticidade dinâmico e estático do concreto. In: Congresso Brasileiro de Engenharia e Ciência dos Materiais, 18º, 2008, Porto de Galinhas – PE, Anais, pp. 941-951.
[28] SALMAN, M. M.; AL-AMAWEE, A. H. The ratio between static and dynamic modulus of elasticity in normal and high strength concrete. Journal of Engineering and Development, v. 10, No. 2, 2006, pp.163-174.
[29] DIÓGENES, H. J. F.; COSSOLINO, L. C.; PEREIRA, A. H. A.; EL DEBS, M. K.; EL DEBS, A. L. H. C. Determinação do módulo de elasticidade do concreto a partir da resposta acústica. Revista Ibracon de Estruturas e Materiais, v. 4, No. 5, 2011, pp. 792-813.
[30] HAACH, V. G.; CARRAZEDO, R; OLIVEIRA, L. M. F.; CORREA, M. R. S. Application of acoustic tests to mechanical characterization of masonry mortars. NDT&E International, v. 59, 2013, pp. 18-24.
[31] ASTM C666, Standard test method for resistance of concrete to rapid freezing and thawing; designation: C666-97. ASTM International, 2017.
[32] CASTRO, A. L.; LIBORIO, J. B. L.; PANDOLFELLI, V. C. Desempenho de concretos avançados para a construção civil, formulados a partir do método de dosagem computacional. Cerâmica, São Paulo, v. 55, No. 335, 2009, pp. 233-251.
[33] LU, X.; SUN, Q.; FENG, W.; TIAN, J. Evaluation of dynamic modulus of elasticity of concrete using impact-echo method. Construction and Building Materials, v. 47, 2013, pp. 231-239.
[34] HARSH, S.; SHEN, Z.; DARWIN, D. Strain-rate sensitive behavior of cement paste and mortar in compression. ACI Materials Journal, v. 87, No. 5, 1990, pp. 508-516.
[35] POPOVICS, S. Verification of relationships between mechanical properties of concrete-like materials. Matériaux et Constructions, v. 8, Issue 3, 1975, pp. 183-191.
[36] Disponível em: < https://www.sonelastic.com/pt/fundamentos/bases/tecnica-excitacao-impulso.html> Acessado em: 18 de Agosto de 2022.
[37] CALLISTER Jr., W.D. Materials Science and Engineering. 7ª ed. New York: John Wiley & Sons, Inc, 2007.


