Determinação dos módulos de elasticidade do concreto empregando a Técnica de Excitação por Impulso (ABNT NBR 8522-1&2:2021)
O objetivo desta seção é apresentar a teoria e a metodologia para a determinação não-destrutiva do módulo elasticidade dinâmico de concretos (Ecd) pela Técnica de Excitação por Impulso [1] e para a estimativa do módulo de deformação tangente inicial (Eci) a partir do Ecd. É apresentada uma revisão da literatura e os avanços normativos que ocorreram no Brasil com a publicação da norma ABNT NBR 8522-1&2:2021 [2].
Introdução
Os módulos de elasticidade são propriedades fundamentais e, cada vez mais, projetistas especificam valores mínimos a serem atendidos por conta da evolução da resistência à compressão axial dos concretos. Até recentemente, não havia consenso sobre a metodologia ideal para o controle rotineiro dessas propriedades, bem como uma metodologia de ensaio normatizada que fosse prática e econômica. Face a estas dificuldades, os módulos de elasticidade acabavam sendo medidos raramente ou estimados com incerteza considerável a partir da resistência à compressão. Essa realidade está mudando com os avanços proporcionados pela publicação da ABNT NBR 8522-1&2:2021 [2], que normatizou os métodos baseados nas frequências naturais de vibração e a estimativa do Eci a partir do Ecd. Os métodos das frequências naturais de vibração, em particular a Técnica de Excitação por Impulso (TEI) [1,2], são mais precisos, práticos e acessíveis para a determinação do módulo de elasticidade do concreto do que os métodos estáticos [2]. Adicionalmente, permitem a medição não-destrutiva destas propriedades nos mesmos corpos de prova a serem ensaiados para a determinação da resistência à compressão.
O concreto é um material compósito, no qual partículas ou fragmentos de agregados estão aglutinados por uma matriz [3]. Quando a matriz ou os agregados são solicitados individualmente, ambos apresentam uma curva tensão-deformação linear que possibilita a determinação do módulo de elasticidade estático com facilidade; entretanto, o concreto não apresenta tal linearidade devido à presença e ao surgimento de trincas e microtrincas na interface da matriz com os agregados [3,4].
Os concretos podem ser classificados em função da resistência característica à compressão axial (fck), sendo aqueles com fck até 20 MPa denominados concretos de baixa resistência, com fck entre 20 MPa e 40 MPa, concretos de resistência média, e os com fck maior que 40 MPa, concretos de alta resistência [3]. A Fig. 1 mostra um exemplo de aplicação de concreto de alta resistência, o edifício Leopoldo 1201. Construído em São Paulo no ano de 2021, este edifício empregou concreto com módulo de elasticidade recorde de 48 GPa desenvolvido pela PhD Engenharia em conjunto com a Engemix e a Nortis.

Figura 1 – Construção do edifício Leopoldo 1201, que empregou concreto com módulo de elasticidade recorde de 48 GPa (2021) [8].
É usual estimar o Eci do concreto a partir da resistência a compressão axial empregando modelos empíricos [3,4]. Entretanto, apesar destes modelos poderem oferecer uma estimativa razoável, há duas fontes de incerteza importantes que devem ser levadas em consideração: a primeira é a validade e as limitações do modelo empregado [3,4], que depende da classificação do concreto; a segunda é a alta dispersão dos resultados dos ensaios para a caracterização da resistência à compressão. Uma alternativa prática, de baixo custo e recentemente normatizada, é a estimativa do Eci a partir do módulo de elasticidade dinâmico do concreto (Ecd) empregando-se o modelo de Popovics [2,5-7]. Para a determinação do Ecd é empregada a Técnica de Excitação por Impulso (TEI) [1,2]. A TEI é baseada nas frequências naturais de vibração do corpo de prova e, ao contrário dos ensaios estáticos, leva poucos minutos, tem baixa incerteza (≈1,5%) e alta reprodutibilidade (≈0,6%) [1,2]. Nesse caso, ambas as propriedades (Eci e Ecd) estão relacionadas somente às características elásticas do material e o ponto de partida é uma propriedade mensurável com exatidão e de forma não-destrutiva [2,6,7]. A Figura 2 mostra uma aplicação de concreto com módulo de elasticidade definido e dimensionado para estruturas esbeltas e grandes vãos [9].

Figura 2 - Aplicação de concreto com módulo de elasticidade definido e dimensionado especificamente para estruturas esbeltas e grandes vãos [9].
Quando comparada a métodos fundamentados na velocidade de ondas ultrassônicas, a Técnica de Excitação por Impulso apresenta vantagens expressivas para a caracterização dos módulos de elasticidade do concreto, por exemplo, não é necessário o acoplamento de transdutores no corpo de prova e os resultados são muito menos sensíveis à habilidade do operador e à estimativa do coeficiente de Poisson [7]. Adicionalmente, a Técnica de Excitação por Impulso permite a caracterização simultânea do amortecimento ou atrito interno, não demanda de calibrações constantes e é menos influenciada pelo tamanho dos agregados.
A construção civil é o principal setor consumidor de concreto e é altamente competitiva e dinâmica. Avanços tecnológicos e de normatização que aprimorem e facilitem o controle tecnológico do concreto são altamente bem vindos para todos os envolvidos (projetistas, construtoras, empresas de serviço de concretagem e laboratórios).
Os módulos de elasticidade do concreto
De forma geral, o módulo de elasticidade, ou módulo de Young, consiste no coeficiente de proporcionalidade entre a tensão e a deformação durante o regime elástico do material. Entretanto, a curva tensão-deformação do concreto é não-linear e o coeficiente angular varia com a tensão e com o ajuste da curva, por exemplo, o módulo pode ser de deformação tangente inicial (Eci) ou de deformação secante (Ecs). A denominação também depende do regime da solicitação, que pode ser estático ou dinâmico.
A Figura 3 ilustra curvas tensão-deformação típicas do concreto e de seus principais componentes [3]. Apesar do agregado e da matriz apresentarem comportamento linear, o concreto apresenta comportamento não-linear em função da presença de trinca na interface entre a matriz e os agregados.
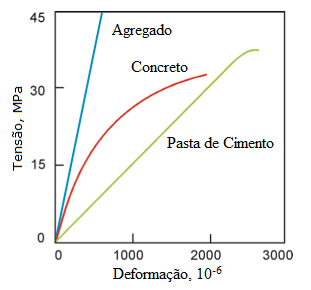
Figura 3 - Comportamento típico da curva tensão-deformação do concreto e de seus principais componentes [3].
As normas nacionais e internacionais descrevem metodologias distintas para a determinação dos módulos de elasticidade estáticos do concreto, de modo que não há um consenso geral sobre como melhor definir, calcular, prever e ensaiar essas propriedades [7]. A partir de ensaios estáticos é possível obter o módulo de elasticidade de deformação tangente inicial e de deformação secante, sendo que ambos podem variar de acordo com os locais da curva tensão-deformação considerados para sua determinação (Fig. 4). Além disso, outros aspectos como os parâmetros experimentais e o tamanho do corpo de prova e ciclos de pré-carregamento podem influenciar diretamente na determinação desta propriedade [3,4].

Figura 4 - Diferentes formas de obter o módulo de elasticidade a partir da curva tensão-deformação [10].
O módulo de elasticidade do concreto também pode ser obtido através de ensaios não-destrutivos, usualmente fundamentados nas frequências naturais de vibração ou na velocidade de propagação de ondas ultrassônicas (o módulo de elasticidade obtido por estes ensaios é classificado como dinâmico) [7,10]. O emprego de ensaios não-destrutivos possui vantagens relevantes, como a alta exatidão e a possibilidade de se submeter o mesmo corpo de prova a outros ensaios, o que torna possível acompanhar a evolução do módulo de elasticidade ao longo de processos de cura, de processos de degradação e em função da umidade e da temperatura. Desta forma, reduz-se a incerteza dos resultados e a quantidade total de corpos de prova necessários para um mesmo estudo.
Ao contrário dos ensaios mecânicos estáticos, os ensaios dinâmicos submetem o material a baixos níveis de tensão, de forma que é desprezível a probabilidade de efeitos relacionados à fluência e a indução ou crescimento de microtrincas no material. Por estas razões, o módulo dinâmico está mais próximo do módulo de deformação tangente inicial, o qual é obtido no início da curva tensão-deformação.
O módulo de elasticidade em regime dinâmico é sempre maior do que os módulos obtidos em regime estático, em torno de 20% para os concretos de alta resistência, 30% para os concretos de média resistência e 40% para os concretos de baixa resistência [3]. Isso ocorre porque a solicitação do material no regime dinâmico ocorre em intervalos de tempo menores do que o tempo de relaxação do concreto.
Parâmetros que influenciam o módulo de elasticidade do concreto
As propriedades elásticas do concreto dependem em grande parte das propriedades de seus componentes e das propriedades da interface entre a matriz e os agregados. Além destes, há fatores externos que podem influenciar o modulo de elasticidade, por exemplo, a umidade do corpo de prova. A Figura 5 descreve os principais parâmetros que afetam o módulo de elasticidade dos concretos.
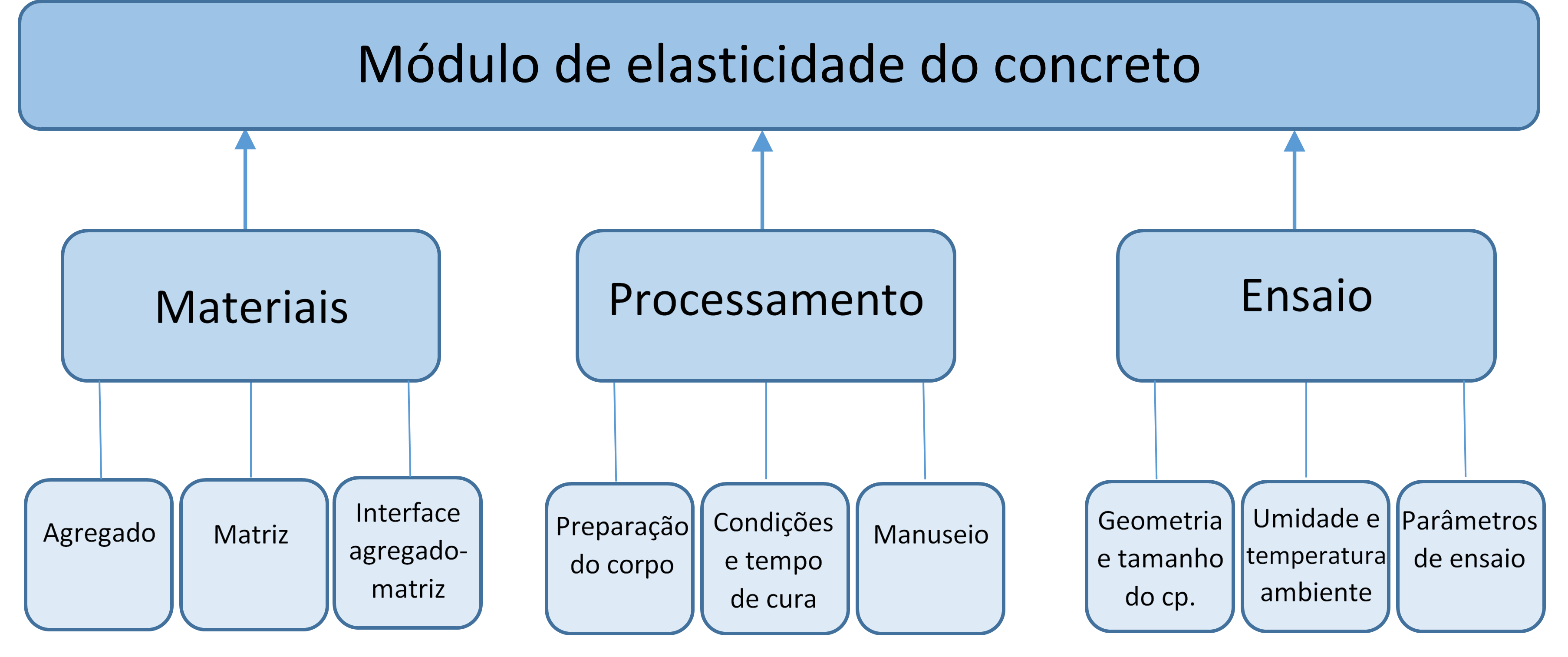
Figura 5 - Parâmetros que influenciam o módulo de elasticidade dos concretos.
• Agregado
O módulo de elasticidade do agregado é geralmente maior que o módulo da pasta de cimento (matriz), sendo a porosidade uma das principais variáveis. Quanto maior a porosidade de um agregado, menor será o seu módulo de elasticidade e do concreto no qual foi empregado (Fig. 6) [3]. Por exemplo, agregados de alta densidade (baixa porosidade) como o granito, o basalto e as rochas vulcânicas possuem módulo de elasticidade maior do que agregados de baixa densidade (porosos), como arenitos, calcários e cascalhos.
A variação na porosidade dos agregados influencia o módulo de elasticidade do concreto, porém não afeta de forma significativa a resistência à compressão, principalmente para concretos de baixa e média resistência. Este fato demonstra um dos exemplos em que a influência de uma variável não é a mesma para a resistência mecânica e para o módulo de elasticidade, o que explica a dificuldade em se encontrar um modelo geral que correlacione o módulo de elasticidade com a resistência à compressão [3].
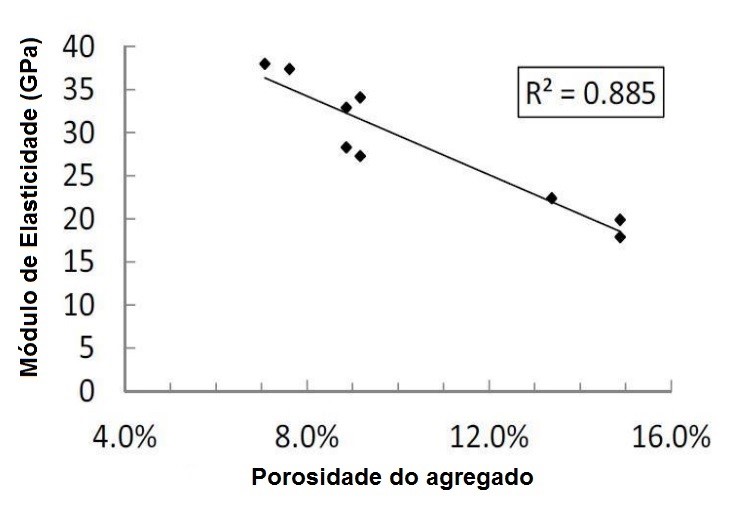
Figura 6 - Influência da porosidade do agregado no módulo de elasticidade do concreto (gráfico adaptado [11]).
A forma, o tamanho médio, a textura superficial, a presença de finos e a composição mineralógica dos agregados também influenciam o módulo de elasticidade do concreto. Estes fatores afetam a zona de interface entre a matriz e os agregados, determinando a tendência à fissuração desta região [3,4]. Além disso, a fração volumétrica de agregado utilizado na mistura também irá afetar o módulo de elasticidade do concreto.
• Matriz
Assim como para os agregados, o módulo de elasticidade da pasta de cimento está diretamente relacionado a porosidade, o qual, por sua vez, influenciará nas propriedades do concreto. A porosidade final da matriz é determinada por diversos parâmetros, sendo os principais a relação água/cimento (Fig. 7), o teor de ar incorporado, as adições minerais e o grau de hidratação do cimento.
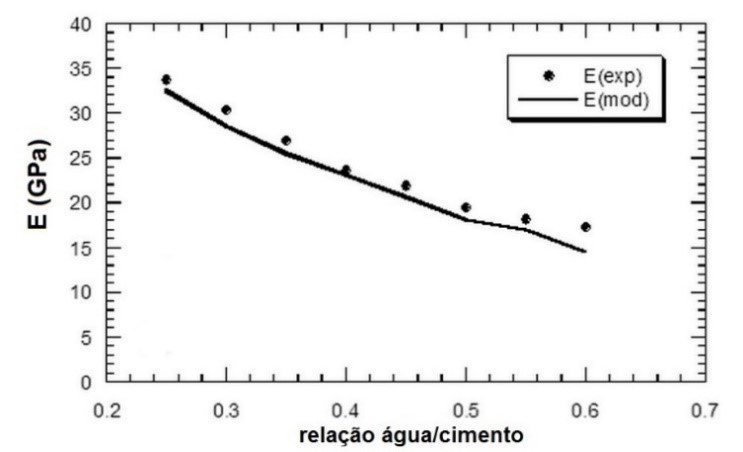
Figura 7 - Influência da relação água/cimento no módulo de elasticidade (gráf. adaptado [12]).
A hidratação das fases do cimento durante o processo de cura influencia na porosidade final da matriz, sendo que os principais vazios encontrados nesta região são decorrentes de espaços não ocupados pelos produtos da reação de hidratação e também devido à presença de ar incorporado.
• Processamento
O processamento de um corpo de prova de concreto envolve a mistura da quantidade correta de matéria-prima, a moldagem, a cura, a retirada dos moldes e o acabamento final dos corpos de prova (capeamento ou retificação). Durante a preparação, o processo de cura deve ser controlado (a Fig. 8 ilustra a influência da temperatura de cura no módulo de elasticidade), assim como deve-se garantir que não haja segregação entre os componentes. O cuidado com o armazenamento e o transporte dos corpos de prova também são importantes, a falta de controle destas variáveis pode comprometer os resultados.
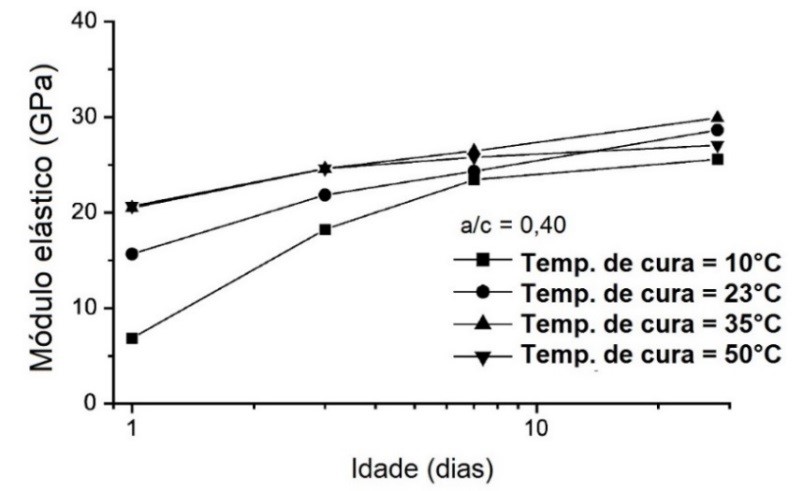
Figura 8 - Módulo de elasticidade em função da idade e da temperatura de cura (gráfico adaptado [13]).
• Ensaio
As condições do corpo de prova devem ser avaliadas antes do ensaio, visto que suas propriedades podem ser afetadas pelas variáveis ambientais. Por exemplo, o módulo de elasticidade em condições úmidas pode ser cerca de 15% maior do que em condições secas [3]. Para ensaios estáticos, uma variável importante é a velocidade de carregamento, devem ser empregadas velocidades intermediárias. Para velocidades muito baixas, o fenômeno da fluência do concreto reduzirá o módulo de elasticidade; por outro lado, velocidades muito altas podem levar a resultados superestimados [14].
A norma ABNT NBR 8522-1&2:2021 [2] determina que os corpos de prova para o ensaio do módulo de elasticidade sejam cilindros com uma razão de 2:1 entre a altura e o diâmetro. É importante mencionar que existem normas estrangeiras semelhantes que especificam outras geometrias. Não é recomendável a comparação de resultados obtidos com corpos de prova de dimensões ou geometrias distintas [2-4,7].
Metodologias para a determinação dos módulos do concreto
• Ensaios estáticos
A norma ABNT NBR 8522-1&2:2021 [2] descreve duas metodologias estáticas e uma dinâmica para a determinação dos módulos de elasticidade do concreto, e sugere o emprego de corpos de prova cilíndricos preparados com a proporção de 2:1 entre a altura e o diâmetro, conforme ABNT NBR 5738:2015 [15].
A primeira metodologia estática descreve a obtenção do módulo de deformação secante (Ecs), definido como o coeficiente angular da reta secante à curva tensão-deformação passando por dois pontos do gráfico, em que o primeiro corresponde à tensão de 0,5 MPa e o segundo na tensão desejada. A segunda metodologia descreve a obtenção do módulo de deformação tangente inicial (Eci), o qual, segundo a definição da norma, é considerado equivalente ao módulo de elasticidade secante entre uma tensão fixa (σa = 0,5 MPa) e 30% da resistência à compressão do concreto. Para os métodos estáticos, recomenda-se ciclos de pré-carga para a acomodação do corpo de prova na máquina de ensaio antes de se registrar os valores de tensão e deformação (Fig. 9).

Figura 9 - Procedimento de pré carregamento da ABNT NBR 8522-1:2021 [2].
É importante ressaltar que não há consenso quanto aos parâmetros de ensaio que devem ser aplicados para a determinação do módulo de elasticidade estático. Normas nacionais e internacionais apresentam diferenças significativas em parâmetros que afetam o resultado final, como a taxa de carregamento, o número de pré-carregamentos, a tensão máxima, a geometria e a dimensões. Além disso, a determinação da deformação no início da curva tensão-deformação é difícil devido à presença de imperfeições nas superfícies dos corpos de prova e acomodação da máquina de ensaio [16]. Ensaios interlaboratoriais demonstraram que o coeficiente de variação desta propriedade é de 10% a 15% [6,17]. Portanto, recomenda-se fornecer informações sobre o procedimento adotado no ensaio ao se reportar o módulo de elasticidade de determinado corpo de prova de concreto.
• Estimativa do módulo de elasticidade pela resistência à compressão
Existem modelos empíricos que permitem estimar o módulo de elasticidade a partir da resistência à compressão axial. Esses modelos devem ser usados com cautela, visto que a resistência à compressão e o módulo de elasticidade são propriedades mecânicas distintas e influenciadas diferentemente pelas variáveis do concreto [3,4]. Não há um consenso sobre qual o melhor modelo de previsão do módulo de elasticidade a partir da resistência a compressão, visto que há questionamentos sobre as normas nacionais e internacionais que aplicam esta abordagem [6,18-20]. A Figura 10 ilustra os resultados dos principais modelos utilizados para previsão do módulo de elasticidade de concretos a partir da resistência à compressão.

Figura 10 - Modelos disponíveis em normas para a previsão do módulo de elasticidade a partir da resistência à compressão axial.
Usualmente, o módulo de elasticidade é especificado em projeto através de uma correlação com sua resistência à compressão. Em função disso, não é rara a situação em que o fornecedor de concreto é obrigado a fabricar um material com uma resistência à compressão maior do que a especificada para compensar a incerteza da estimativa do módulo de elasticidade estático e não correr o risco de ter o material reprovado [19,21].
A seguir estão representadas as principais equações que correlacionam a resistência à compressão com o módulo de elasticidade do concreto de acordo com as respectivas normas:
- Associação Brasileira de Normas Técnicas – Norma Brasileira 6118 (ABNT NBR 6118:2014) [22]:

- Fédération internationale du béton -Model Code for Concrete Structures 2010 (fib MODEL CODE 2010) [23]:
Para ambos os modelos, Eci refere-se ao módulo de deformação tangente inicial aos 28 dias, αE é uma constante adimensional que depende do tipo de agregado utilizado para a fabricação do concreto (Tabela 1) e fck é a resistência característica do concreto à compressão.
Tabela 1 - Valor de αE de acordo com o tipo de agregado utilizado na fabricação do concreto.

- American Concrete Institute – 318: Building code requirements for structural concrete (ACI 318) [24]

Em que Ec é o módulo de elasticidade secante obtido a partir do ponto inicial até um nível de tensão igual a 0,45fc, ωc é a densidade do concreto (em kg/m³) e fc é a resistência à compressão especificada.
- European Committee for Standardization. Eurocode 2: Design of Concrete Structures (EUROCODE 2) [25]
Em que Ecm é o módulo de elasticidade secante obtido a partir do ponto inicial até um nível de tensão igual a 0,4fcm e fcm é a resistência média à compressão.
Metodologia para determinação do Ecd e estimativa do Eci
Ensaios dinâmicos e a Técnica de Excitação por Impulso (TEI)
Uma alternativa prática, precisa e acurada para a obtenção do módulo de deformação tangente inicial de um corpo de prova de concreto é a estimativa a partir do módulo de elasticidade dinâmico obtido pelas frequências naturais de vibração [7]. Adicionalmente, o módulo de elasticidade dinâmico é especialmente relevante para aplicações em que o concreto é submetido a cargas dinâmicas, por exemplo, em aplicações onde ocorrem carregamentos súbitos da estrutura [26]. Por serem aplicadas tensões muito pequenas durante a determinação desta propriedade, não há a indução de microtrincamento, assim como não há o efeito de fluência. Por esta razão, pode-se considerar que o módulo dinâmico está associado a fenômenos puramente elásticos [4].
A Parte 2 da norma ABNT NBR 8522-1&2:2021 estabelece o método de ensaio para a determinação do módulo de elasticidade dinâmico de corpos de prova de concreto pelas frequências naturais de vibração [2]. A informação da frequência, juntamente com a massa e as dimensões, permite o cálculo do módulo de elasticidade dinâmico (Ecd). Caso a excitação do corpo de prova seja por impacto, esta variação é denominada por Técnica de Excitação por Impulso (TEI) [1,2]. A adoção da TEI tem-se popularizado no desenvolvimento e no controle tecnológico do concreto para a estimativa do módulo de deformação tangente inicial [6,7,27-30], segue abaixo as principais vantagens da TEI:
- Permite reduzir a quantidade total de corpos de prova e intercalar o ensaio com outros processos por ser uma técnica não-destrutiva;
- Proporciona resultados mais exatos que os ensaios estáticos devido ao menor número de variáveis e menor susceptibilidade a erros experimentais [27,30];
- Agiliza a obtenção dos resultados visto que a caracterização leva poucos minutos e pode ser repetida quantas vezes for desejado;
- Torna possível acompanhar o módulo de elasticidade em função do tempo, por exemplo, ao longo de processos de cura (Fig. 11);
- Possibilita avaliar danos progressivos, visto que a fissuração diminui a rigidez do material e, consequentemente, reduz a frequência natural de vibração [26];
- Torna possível acompanhar a variação do módulo de elasticidade de corpo de prova em função de outras variáveis, como a temperatura e o número de ciclos térmicos (norma ASTM C666 [31]).
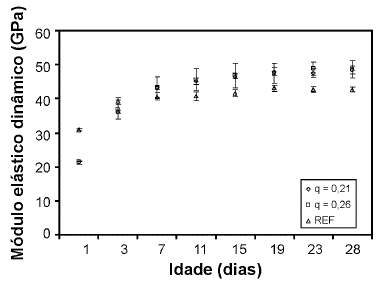
Figura 11 - Acompanhamento do módulo de elasticidade dinâmico de três corpos de prova distintos em função da idade [32].
Relação entre os módulos de elasticidade estático e o dinâmico
A diferença entre os módulos de elasticidade estático e o módulo de elasticidade dinâmico de um concreto deve-se ao caráter viscoelástico do material, que causa a mudança de comportamento com a variação da taxa de deformação (Fig. 12).

Figura 12 – Curvas obtidas a partir de modelos teóricos demonstrando a influência da taxa de deformação nas curvas tensão-deformação de um concreto [14].
Quanto menor a taxa de deformação aplicada, maior será o tempo para a acomodação das tensões e menor a inclinação da curva tensão-deformação. Por outro lado, quanto maior a taxa, menor será o tempo para a acomodação das tensões e maior a inclinação da curva tensão-deformação (Fig. 12). A taxa de deformação aplicada durante um ensaio dinâmico é sempre superior à aplicada em um ensaio estático, assim como os níveis de deformação aplicados em um ensaio dinâmico são menores. Em função disso, o módulo de elasticidade dinâmico será sempre maior ou igual ao obtido em um ensaio estático [14,33,34].
Abaixo é apresentada a equação estabelecida no Anexo B da Parte 1 da ABNT NBR 8522-1&2:2021 para a estimativa do módulo de elasticidade tangente inicial (Eci) a partir do módulo dinâmico (Ecd). Esta equação consiste no modelo de Popovics [35] e leva em consideração a densidade do concreto.
Em que ρ é a densidade do concreto em kg/m³ e k uma constante que depende das unidades utilizadas (k=0,107 quando o módulo é dado em Pa e a densidade em kg/m³).
Tabela 2 – Módulo de deformação tangente inicial (Eci) estimado em função do módulo de elasticidade dinâmico (Ecd) do concreto para diferentes densidades empregando-se o modelo de Popovics [35] conforme Anexo B da Parte 1 da ABNT NBR 8522-1&2:2021 [2].
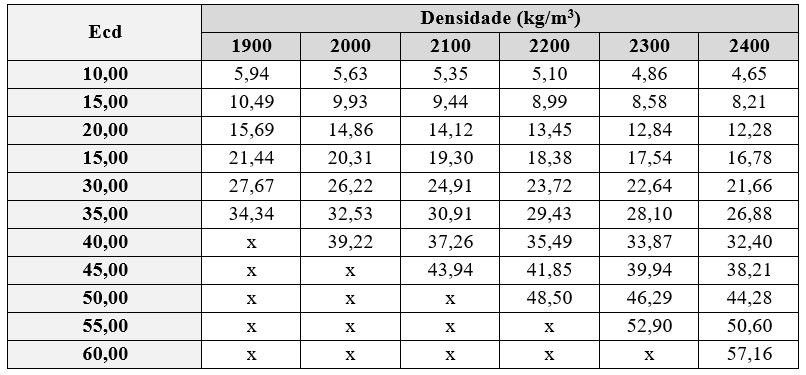
A Tabela 2 apresenta os valores de Eci estimados para concretos com densidade entre 1900 e 2400 kg/m3 e módulo de elasticidade dinâmico (Ecd) entre 10 e 60 GPa. O módulo dinâmico é sempre maior ou igual ao estático. A incerteza dessa estimativa é de aproximadamente 13% [2].
Passo a passo para a estimativa do Eci empregando a TEI
A seguir é apresentado o passo a passo para a estimativa do Eci de um corpo de prova de concreto a partir do módulo de Ecd obtido pela Técnica de Excitação por Impulso.
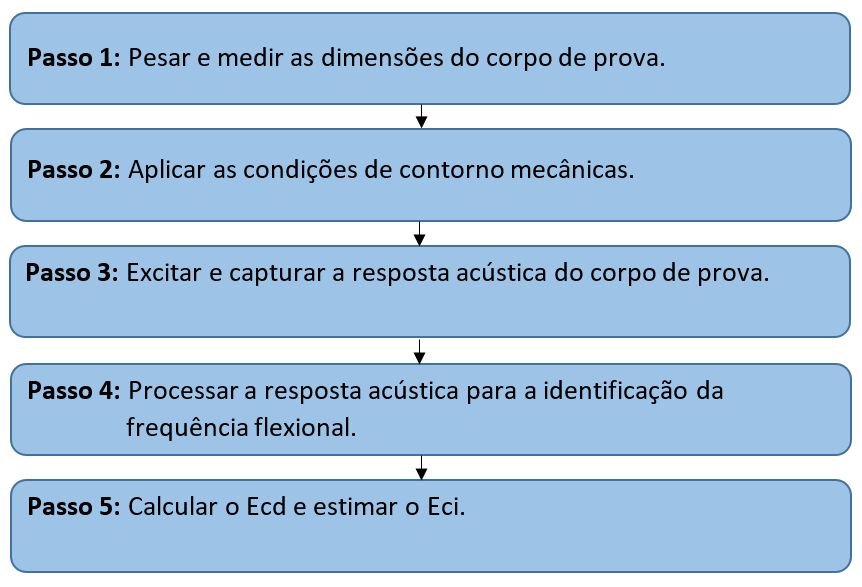
Figura 13 - Fluxograma para a estimativa do Eci empregando a Técnica de Excitação por Impulso.
Passo 1 - Pesar e medir as dimensões do corpo de prova:
O primeiro passo consiste em pesar e medir as dimensões do corpo de prova. Os corpos de prova típicos são cilindros com 200 mm de altura e 100 mm de diâmetro. A altura deve ser igual a média entre a medição máxima e mínima, o diâmetro deve ser igual a média de duas medições ortogonais tomadas a meia altura [2].
Passo 2 – Aplicar as condições de contorno mecânicas:
O segundo passo consiste em apoiar o corpo de prova nas posições iguais a 0,224h da extremidade (h é a altura) e posicionar o captador acústico e o dispositivo de impacto em lados opostos no centro do corpo de prova em relação ao plano de vibração.
Passo 3 – Excitar e capturar a resposta acústica do corpo de prova:
O terceiro passo consiste na excitação do corpo de prova com a aplicação de um impacto único e captura da resposta acústica correspondente com um captador acústico. Recomendamos a utilização do Sistema Sonelastic® mostrada na Figura 14.

Figura 14 - Sistema Sonelastic® para corpos de prova de concreto: Computador com o Software Sonelastic®, digitalizador de sinais ADAC, captador acústico CA-DP, suporte para barras e cilindros SA-BC e pulsador manual médio.
Passo 4 – Processar a resposta acústica para a identificação da frequência:
O quarto passo consiste em processar a resposta acústica para a identificação da frequência flexional. Este processamento é realizado automaticamente pelo Software Sonelastic®.
Passo 5 – Cálculo do Ecd e estimativa do Eci:
O quinto e último passo consiste no cálculo do Ecd conforme Parte 2 da ABNT 8522:2021 e aplicação do modelo de Popovics conforme Anexo B da Parte 1 da mesma norma para a estimativa do Eci [2]. Segue abaixo a equação do modelo de Popovics:
Os valores de entrada correspondem à densidade do concreto (ρ) em kg/m³ e ao módulo de elasticidade dinâmico (Ecd) em Pa.
Também pode-se elaborar um relatório dos resultados. Além de especificar a norma utilizada [2], este relatório deve conter todos os dados que podem afetar os resultados (material, processamento, cura, geometria do corpo de prova, idade e condições do ensaio).
Detalhamento da determinação do Ecd pela TEI
Fundamentos da técnica
A Técnica de Excitação por Impulso descrita na Parte 2 da ABNT NBR 85221&2:2021 [2] consiste essencialmente na determinação do módulo de elasticidade do concreto a partir da frequência natural de vibração de um corpo de prova cilíndrico no modo flexional fundamental. Esta frequência é excitada com um impacto mecânico de curta duração, seguido da captação da resposta acústica por um captador acústico. Um tratamento matemático (Transformada Rápida de Fourier) é aplicado pelo Software para a obtenção do espectro de frequências e identificação da frequência flexional. A partir disso, o módulo dinâmico é calculado através da equação prevista na norma considerando a geometria, a massa, as dimensões do corpo de prova e a frequência [2].
Para a excitação do modo de vibração desejado é necessário impor condições de contorno específicas. Na Figura 15 é apresentado um exemplo de apoio de corpo de prova cilíndrico nas linhas nodais, de posição da excitação e de captação da resposta acústica para o modo flexional fundamental [36].
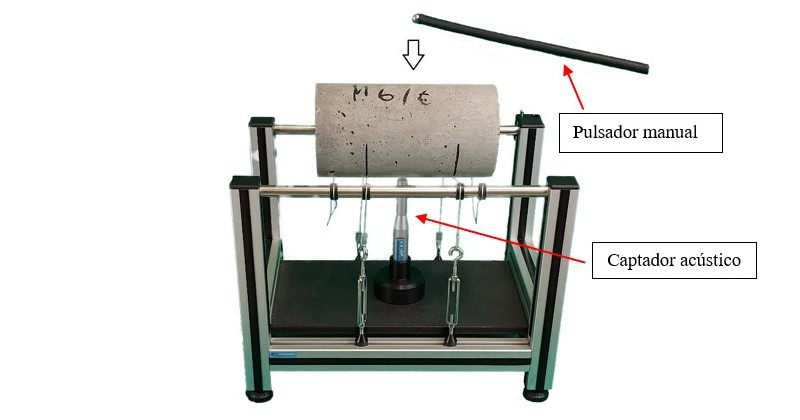
Figura 15 – Disposição para a determinação do módulo de elasticidade dinâmico de um corpo de prova cilíndrico de concreto de acordo com a ABNT NBR 8522-1&2:2021 [2] e empregando o Sistema Sonelastic®.
Modos de vibração
Um corpo de prova pode vibrar em diferentes modos e para cada modo há uma frequência fundamental característica. Na Figura 16 são apresentados os principais modos fundamentais de vibração de um cilindro e de um disco.
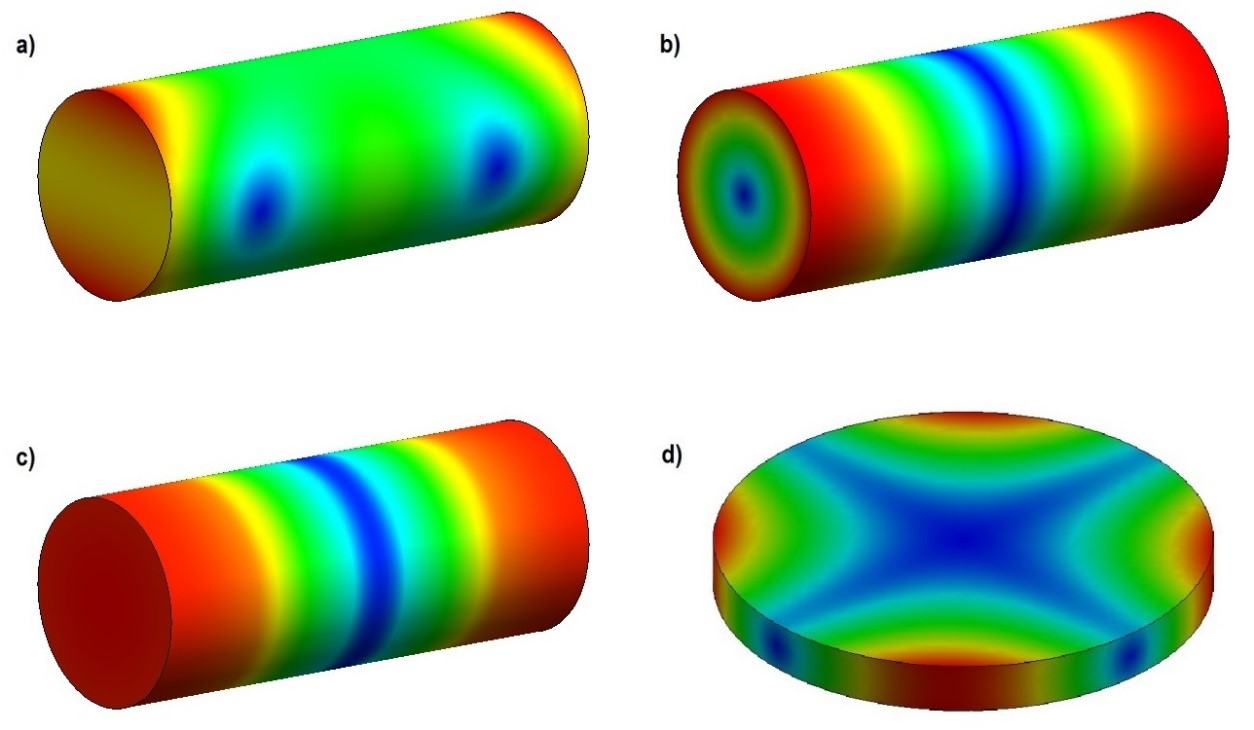
Figura 16 - Modos fundamentais de vibração: a) Flexional, b) Torcional, c) Longitudinal e d) Planar. As regiões em azul representam os pontos em que a amplitude de vibração é mínima, enquanto as regiões em vermelho representam as regiões em que a amplitude de vibração é máxima.
O que determina qual modo de vibração será excitado são as condições de contorno impostas, no apoio, excitação e captação da resposta acústica. A frequência fundamental destes modos depende da geometria, da massa, das dimensões e dos módulos elásticos do material.
Nas Figuras 17a-c estão representadas as condições de contorno ótimas para se obter as frequências naturais de vibração dos principais modos de vibração de um cilindro [1]. O módulo de elasticidade dinâmico é calculado empregando as equações descritas pela norma ASTM E1876 [1] e ABNT NBR 8522-1&2:2021 [2] a partir das frequências de ressonância do corpo de prova, de sua massa e dimensões.
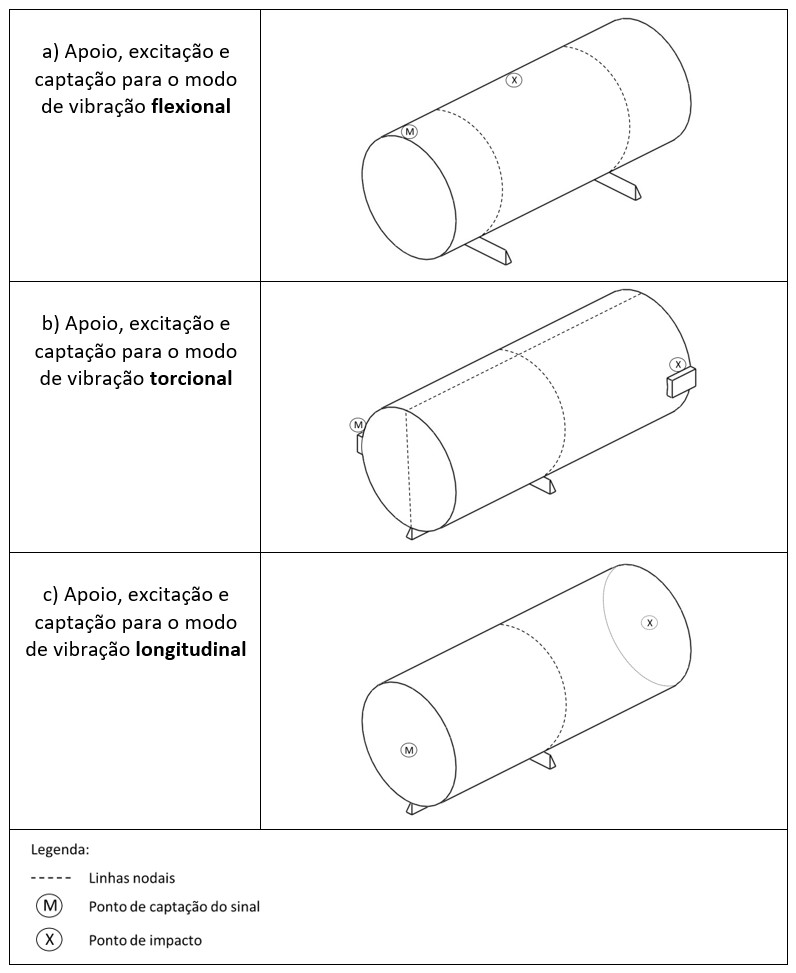
Figura 17 - Condições de contorno impostas ao corpo de prova para a excitação do modo de vibração fundamental flexional (a), torcional (b) e longitudinal (c) [1].
As propriedades elásticas e os modos de vibração
De uma forma geral, as principais propriedades elásticas de um material são o módulo de elasticidade (ou módulo de Young), o módulo de cisalhamento e o coeficiente de Poisson. A Técnica de Excitação por Impulso permite a caracterização destas três propriedades detalhadas a seguir em função do modo de vibração aplicado.
• Módulo de elasticidade
- Modo de vibração longitudinal: Quando o corpo de prova vibra na direção longitudinal, o módulo de elasticidade medido é referente à direção do comprimento do corpo de prova, ou seja, este módulo é o equivalente dinâmico do valor obtido em um ensaio de tração ou compressão.
- Modo de vibração flexional: Quando um corpo é flexionado, ocorrem solicitações simultâneas de tração e compressão, como mostra a Fig. 18 [37]. Para materiais homogêneos e isotrópicos, o módulo de elasticidade obtido em um ensaio de flexão coincide com o módulo medido na direção longitudinal. Portanto, o módulo de elasticidade dinâmico obtido por meio do modo de vibração flexional é o mesmo que o obtido por meio do modo de vibração longitudinal [37]. Porém, sabe-se que, em flexão, a superfície do material é a região em que estão presentes as maiores tensões. Por essa razão, caso a rigidez do corpo de prova seja diferente na superfície em comparação ao centro (por exemplo, se houver um gradiente de rigidez ao longo da espessura), ou caso o corpo de prova apresente defeitos como poros, trincas e microtrincas em sua superfície, haverá uma discrepância nos valores obtidos pelo modo de vibração flexional e longitudinal. Diversos trabalhos apresentam uma comparação entre o módulo de elasticidade medido a partir dos modos de vibração flexional e longitudinal [5-7].
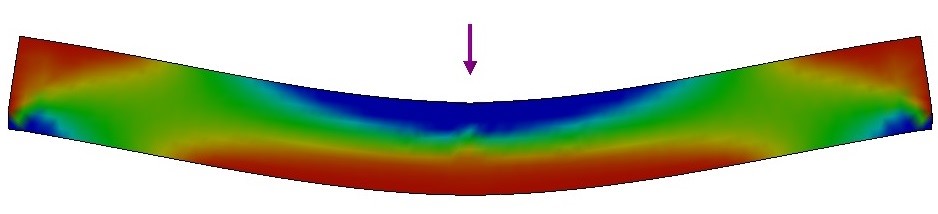
Figura 18 - Região em tração (vermelho) e em compressão (azul) durante um ensaio de flexão.
• Módulo de cisalhamento
- Modo de vibração torcional: Uma das principais formas de obtenção do módulo de cisalhamento em um ensaio estático é através de um ensaio de torção. Na Técnica de Excitação por Impulso, o princípio é semelhante, porém neste caso deve-se proporcionar as condições de contorno para o corpo de prova vibrar no modo torcional (vide Fig. 17b). No caso de corpos de prova retangulares, basta aplicação a excitação próximo a uma das arestas laterais fora das linhas nodais e captar o sinal em um ponto oposto simétrico. Porém, no caso de corpos de prova cilíndricos, é necessário acoplar pequenas abas próximo às extremidades do corpo de prova, de forma a possibilitar a excitação e a captação da resposta acústica na torção.
• Coeficiente de Poisson
A determinação do coeficiente de Poisson pela Técnica de Excitação por Impulso é indireta, a partir da correlação entre o módulo de elasticidade e o módulo de cisalhamento do material [1], e dada pela seguinte expressão:
Em que E é o módulo de elasticidade, G é o módulo de cisalhamento e ν é o coeficiente de Poisson.
Exemplos de clientes e aplicações na área de concretos, materiais cimentícios e rochas.
Referências bibliográficas
[1] ASTM E1876, Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; designation: E1876-21. ASTM International, 2021.
[2] ASTM C215, Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens; designation: C215-19. ASTM International, 2019.
[3] MEHTA, P. K.; MONTEIRO, P. J. M. Concreto: Microestrutura, Propriedades e Materiais. 3 ed. São Paulo: IBRACON, 2008. 674 p.
[4] NEVILLE, A. M. Properties of Concrete. 5th ed. England: Pearson, 2011.
[5] MALHOTRA, V. M.; SIVASUNDARAM, V. Resonant Frequency Methods. In.: MALHOTRA, V. M.; CARINO, N. J. (Eds.). Handbook on Nondestructive Testing of Concrete. West Conshohocken: CRC Press LLC (ASTM International), 2004. p. 7-1 – 7-21.
[6] POPOVICS, J. S. A Study of Static and Dynamic Modulus of Elasticity of Concrete. University of Illinois, Urbana, IL. ACI-CRC Final Report. 2008.
[7] PACHECO, J.; BILESKY, P.; MORAIS, T. R.; GRANDO, F.; HELENE, P. Considerações sobre o Módulo de Elasticidade do Concreto. In: Congresso Brasileiro do Concreto, 56°, 2014, Natal - RN, Anais, IBRACON.
[8] Disponível em:
[9] Disponível em:
[10] ALMEIDA, S. M. Análise do módulo de elasticidade estático e dinâmico do concreto de cimento Portland através de ensaios de compressão simples e de frequência ressonante. 2012. 213 p. Dissertação (mestrado) – Escola de Engenharia, Universidade Federal de Minas Gerais, Belo Horizonte, 2012.
[11] GUÐMUNDSSON, J. G. Long-term creep and shrinkage in concrete using porous aggregate – the effects of elastic modulus. 2013. 80 p. Thesis (Master of Science) - School of Science and Engineering, Reykjavík University, Iceland, 2013.
[12] HAECKER, C. -J. et al. Modeling the linear elastic properties of Portland cement paste. Disponível em:
[13] KIM, J. K.; HAN, S. H.; SONG, Y. C. Effect of temperature and aging on the mechanical properties of concrete: Part I. Experimental results. Cement and Concrete Research, v. 32, 2002, pp. 1087-1094.
[14] SHKOLNIK, I. E. Influence of high strain rates on stress–strain relationship, strength and elastic modulus of concrete. Cement & Concrete Composites, v. 30, 2008, pp. 1000-1012.
[15] ABNT NBR 5738:2015 Concreto - Procedimento para moldagem e cura de corpos de prova. 2015.
[16] ARAÚJO, S. S. Influência do tipo de medição na determinação do módulo estático de elasticidade do concreto. 2011. 212 p. Dissertação (mestrado) – Escola de Engenharia Civil, Universidade Federal de Goiás, Goiânia, 2011.
[17] AHN, N.; YANG, S. An Experimental study of the effect of temperature and age on the properties of concrete. In: Proceedings of the Eastern Asia Society for Transportation Studies, v. 4, 2003, pp. 408-416.
[18] NETO, A. A. M.; HELENE, P. Módulo de elasticidade: dosagem e avaliação de modelos de previsão do módulo de elasticidade de concretos. In: Congresso Brasileiro do Concreto, 44°, 2002, Belo Horizonte - MG, Anais, IBRACON.
[19] BORIN, L. A.; BAUER, R. J. F.; FIGUEIREDO, A. D. Risco de rejeição de concretos devido à não conformidade com os parâmetros normalizados para o módulo de elasticidade. Construindo, Belo Horizonte, v. 4, No. 2, 2012, pp. 79-89.
[20] ARAÚJO, J. M. O módulo de deformação longitudinal do concreto. Rio Grande: Dunas, 2001. 25 p. (Estruturas de Concreto, Número 3).
[21] DE MARCHI, R. D. Estudo sobre a variabilidade do módulo de deformação do concreto associada a fatores intrínsecos à produção do material. 2011. 121 p. Dissertação (mestrado) – Escola Politécnica, Universidade de São Paulo, São Paulo, 2011.
[22] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. ABNT NBR 6118: Projeto de estruturas de concreto - Procedimento. Rio de Janeiro: ABNT, 2014. 238 p.
[23] FÉDÉRATION INTERNATIONALE DU BÉTON. fib Model Code for Concrete Structures 2010. Ernst & Sohn, 2013, 434 p.
[24] ACI 318-02 Building code requirements for structural concrete, ACI Manual of Concrete Practice Part 3: Use of Concrete in Buildings – Design, Specifications, and Related Topics, 443 pp.
[25] EUROPEAN COMMITTEE FOR STANDARDIZATION. EUROCODE 2: design of Concrete Structures: part 1-1: general rules and rules for buildings. EN 1992-1-1. Brussels, Belgium, 2004.
[26] ALMEIDA, S. F.; HANAI, J. B. Análise dinâmica experimental da rigidez de elementos de concreto submetidos à danificação progressiva até a ruptura. Cadernos de Engenharia de Estruturas, São Carlos, v. 10, No. 44, 2008, pp. 49-66.
[27] CANESSO, F. A. C.; CORREA, E. C. S; SILVA, A. P. E.; AGUILAR, M. T. P.; CETLIN, P. R. Módulo de elasticidade dinâmico e estático do concreto. In: Congresso Brasileiro de Engenharia e Ciência dos Materiais, 18º, 2008, Porto de Galinhas – PE, Anais, pp. 941-951.
[28] SALMAN, M. M.; AL-AMAWEE, A. H. The ratio between static and dynamic modulus of elasticity in normal and high strength concrete. Journal of Engineering and Development, v. 10, No. 2, 2006, pp.163-174.
[29] DIÓGENES, H. J. F.; COSSOLINO, L. C.; PEREIRA, A. H. A.; EL DEBS, M. K.; EL DEBS, A. L. H. C. Determinação do módulo de elasticidade do concreto a partir da resposta acústica. Revista Ibracon de Estruturas e Materiais, v. 4, No. 5, 2011, pp. 792-813.
[30] HAACH, V. G.; CARRAZEDO, R; OLIVEIRA, L. M. F.; CORREA, M. R. S. Application of acoustic tests to mechanical characterization of masonry mortars. NDT&E International, v. 59, 2013, pp. 18-24.
[31] ASTM C666, Standard test method for resistance of concrete to rapid freezing and thawing; designation: C666-97. ASTM International, 2017.
[32] CASTRO, A. L.; LIBORIO, J. B. L.; PANDOLFELLI, V. C. Desempenho de concretos avançados para a construção civil, formulados a partir do método de dosagem computacional. Cerâmica, São Paulo, v. 55, No. 335, 2009, pp. 233-251.
[33] LU, X.; SUN, Q.; FENG, W.; TIAN, J. Evaluation of dynamic modulus of elasticity of concrete using impact-echo method. Construction and Building Materials, v. 47, 2013, pp. 231-239.
[34] HARSH, S.; SHEN, Z.; DARWIN, D. Strain-rate sensitive behavior of cement paste and mortar in compression. ACI Materials Journal, v. 87, No. 5, 1990, pp. 508-516.
[35] POPOVICS, S. Verification of relationships between mechanical properties of concrete-like materials. Matériaux et Constructions, v. 8, Issue 3, 1975, pp. 183-191.
[36] Disponível em: < https://www.sonelastic.com/pt/fundamentos/bases/tecnica-excitacao-impulso.html> Acessado em: 18 de Agosto de 2022.
[37] CALLISTER Jr., W.D. Materials Science and Engineering. 7ª ed. New York: John Wiley & Sons, Inc, 2007.
Saiba mais sobre os Sistemas Sonelastic® :
Sistema Sonelastic® para corpos de prova de pequeno porteSistema Sonelastic® para corpos de prova de médio porte
Sistema Sonelastic® para corpos de prova de grande porte
Sistema Sonelastic® customizado e orçamento





