Determinação dos módulos elásticos de materiais compósitos empregando a Técnica de Excitação por Impulso
O objetivo desta seção é apresentar a teoria e a metodologia para a determinação não-destrutiva dos módulos elásticos de materiais compósitos. O conteúdo a seguir compreende uma revisão da literatura e os avanços realizados pela ATCP Engenharia Física na aplicação da Técnica de Excitação por Impulso [1] nessa classe de materiais.
Introdução
A definição de materiais compósitos varia entre diferentes autores dependendo das ponderações e considerações realizadas. De acordo com Chawla [2], para que um material seja classificado como compósito, este deve satisfazer algumas condições. Primeiramente, devem ser materiais manufaturados, ou seja, projetados e produzidos pelo homem; devem consistir em uma combinação adequada de fases distintas física e/ou quimicamente entre si, possuindo uma interface bem definida entre elas; por fim, possuir características que não são atingidas por seus componentes isolados.
Os materiais compósitos intrínsecos são constituídos por pelo menos dois componentes: a matriz, que pode ser cerâmica, metálica ou polimérica, e o reforço, que pode ser na forma de fibras ou partículas. Já os compósitos estruturais podem estar na forma de laminados ou painéis sanduíche (Fig. 1).
![Figura 1 - Classificação dos materiais compósitos [3].](/images/F1-PT-Classificacao-dos-materiais-compositos.jpg)
Figura 1 - Classificação dos materiais compósitos [3].
O advento dos compósitos com maior conteúdo tecnológico iniciou na década de 60 pela demanda por materiais que apresentassem alta resistência e baixa densidade. As aplicações envolveram o setor de construção civil, indústria aeroespacial e de energia [2,4]. Atualmente, os compósitos possuem aplicações em diversos segmentos da indústria, sendo empregados na produção de desde artigos simples, passando por carros [5] a vasos de pressão de alto desempenho (Figura 2).

Figura 2 - Vasos de pressão para gás natural fabricados pela 3M com materiais compósitos.
A determinação dos módulos elásticos de compósitos é crucial para o desenvolvimento, a seleção de materiais e o controle de qualidade, assim como para permitir análises por elementos finitos e cálculos estruturais confiáveis. Uma das técnicas não-destrutivas para a determinação dos módulos elásticos é a Técnica de Excitação por Impulso, foco desta seção do site. A Figura 3 apresenta corpos de prova de CFRP e UHMWPE preparados para a determinação dos módulos de elasticidade pela Técnica de Excitação por Impulso.
![Figura 3 - Corpos de provas de uma blindagem balística de polietileno de ultra alto peso molecular (UHMWPE) e de um painel aeronáutico monolítico de plástico reforçado com fibra de carbono (CFPR). Estes corpos de prova estão preparados para a medição não-destrutiva dos módulos elásticos empregando a Técnica de Excitação por Impulso e os Sistemas Sonelastic®. [6].](/images/F3-PT-Corpos-de-prova-UHMWPE-blindagem-balistica-CFPR-fibra-de-carbono.png)
Figura 3 - Corpos de provas de uma blindagem balística de polietileno de ultra alto peso molecular (UHMWPE) e de um painel aeronáutico monolítico de plástico reforçado com fibra de carbono (CFPR). Estes corpos de prova estão preparados para a medição não-destrutiva dos módulos elásticos empregando a Técnica de Excitação por Impulso e os Sistemas Sonelastic®. [6].
Determinação dos módulos elásticos de compósitos empregando a TEI
Fundamentos da técnica
A Técnica de Excitação por Impulso [1] consiste na determinação dos módulos elásticos de um material a partir das frequências naturais de vibração de um ou mais corpos de prova de geometria regular (barra, cilindro, disco ou anel). Essas frequências são excitadas com um impacto mecânico de curta duração, seguido da captação da resposta acústica por um sensor acústico. Na sequência, aplica-se um tratamento matemático no sinal para a obtenção do espectro de frequências. Os módulos elásticos dinâmicos são calculados considerando a geometria, a massa, as dimensões do corpo de prova e as frequências identificadas no espectro da resposta acústica [1].
Para a excitação do modo de vibração desejado, é necessário impor condições de contorno específicas. Na Figura 4 é apresentado um exemplo de suporte de corpo de prova, com pulsador manual e captador acústico posicionados para medir o módulo de Young pelo modo de vibração flexional.
![Figura 4 - a) Disposição básica para a caracterização de uma barra no modo de vibração flexional pela Técnica de Excitação por Impulso [7]; b) Suporte ajustável para barras e cilindros SA-BC desenvolvido e fabricado pela ATCP Engenharia Física com um corpo de prova de compósito aeronáutico.](/images/F4-A-PT-Disposicao-caracterizacao-barra-modo-vibracao-flexional-Tecnica-Excitacao-Impulso-elastico.png)
![Figura 4 - a) Disposição básica para a caracterização de uma barra no modo de vibração flexional pela Técnica de Excitação por Impulso [7]; b) Suporte ajustável para barras e cilindros SA-BC desenvolvido e fabricado pela ATCP Engenharia Física com um corpo de prova de compósito aeronáutico.](/images/F4-B-PT-Barra-modo-vibracao-flexional-Tecnica-Excitacao-Impulso-Suporte-SA-BC-G2-Sonelastic.jpg)
Figura 4 - a) Disposição básica para a caracterização de uma barra no modo de vibração flexional pela Técnica de Excitação por Impulso [7]; b) Suporte ajustável para barras e cilindros SA-BC desenvolvido e fabricado pela ATCP Engenharia Física com um corpo de prova de compósito aeronáutico.
Modos de vibração
Um corpo de prova pode vibrar em diferentes modos e para cada modo há uma frequência fundamental. Na Figura 5 são apresentados os principais modos fundamentais de vibração de uma barra retangular e de um disco [8].
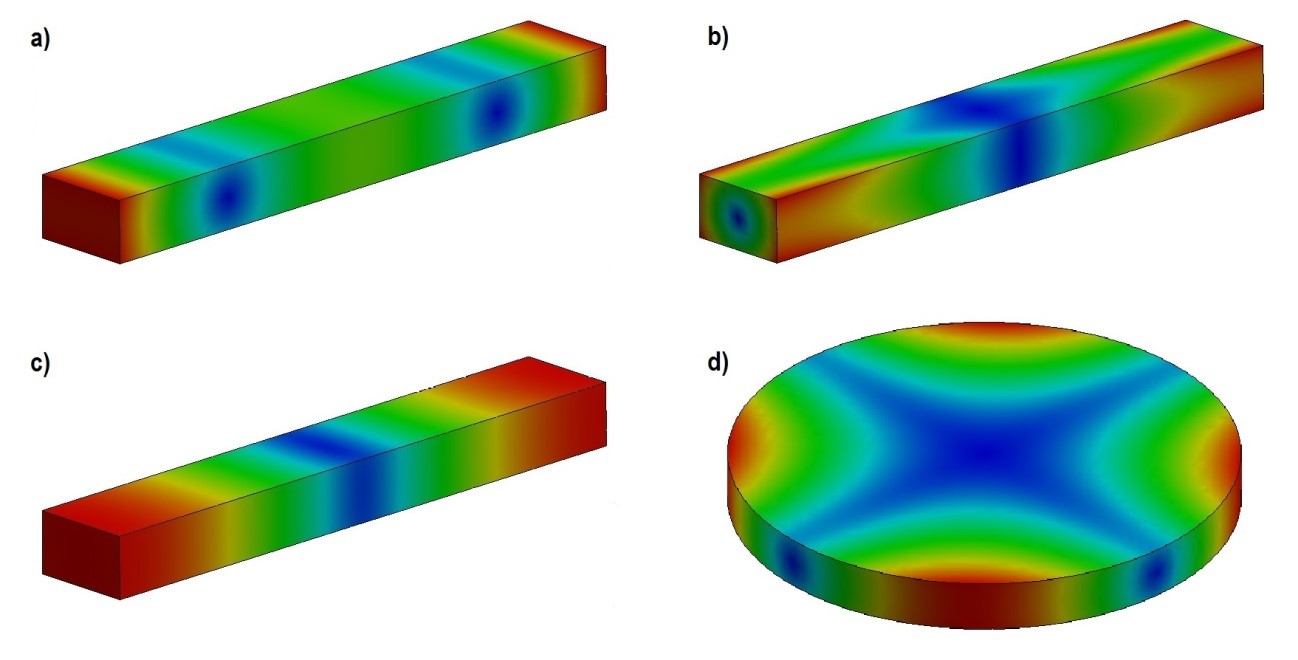
Figura 5 - Modos fundamentais de vibração: a) Flexional, b) Torcional, c) Longitudinal e d) Planar. As áreas em azul representam as regiões em que a amplitude de vibração é mínima, enquanto as áreas em vermelho representam as regiões em que a amplitude de vibração é máxima.
A frequência fundamental destes modos é determinada pela geometria, massa, dimensões e módulos elásticos. O que determina qual modo de vibração será excitado são as condições de contorno impostas ao corpo de prova. Nas Figuras de 6.a a 6.c são ilustradas as condições de contorno ótimas para os principais modos de vibração de uma barra [1] e na Figura 6.d, de um disco. A partir das frequências de ressonância do corpo de prova e empregando as equações descritas pela norma ASTM E1876 [1], são calculados os módulos elásticos dinâmicos correspondentes.
![Figura 6 – Apoio, excitação e captação para os modos de vibração fundamentais (a) Flexional, (b) Torcional, (c) Longitudinal e (d) Planar [1].](/images/F6-PT–Apoio-excitacao-captacao-modos-vibracao-flexional-torcional-longitudinal.jpg)
Figura 6 – Apoio, excitação e captação para os modos de vibração fundamentais (a) Flexional, (b) Torcional, (c) Longitudinal e (d) Planar [1].
Os módulos elásticos dos compósitos
A maioria dos materiais compósitos apresenta algum grau de anisotropia, ou seja, apresenta propriedades dependentes da direção de solicitação. Quando mensurados empregando a Técnica de Excitação por Impulso, é importante conhecer e reportar a simetria do material e a orientação do corpo de prova.
O Apêndice A do Informativo técnico-científico ITC-06 descreve a teoria da elasticidade aplicada aos materiais compósitos a partir de uma visão micro e macromecânica de forma geral, para as três principais simetrias. A Figura 7 ilustra uma estrutura genérica não-isotrópica, tal que, para a determinação dos módulos elásticos principais (E1, E2, E3) são necessários três corpos de prova com orientações nas direções 1, 2 e 3.
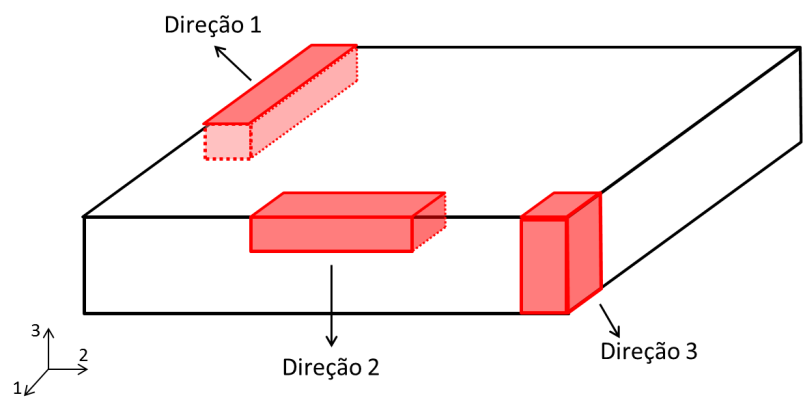
Figura 7 - Ilustração de um material genérico e de como se obter os corpos de prova nas três direções principais.
A Tabela 1 indica os módulos elásticos que podem ser determinados empregando a Técnica de Excitação por Impulso e as orientações relativas a um corpo de prova ortotrópico (Figura 7). Nesta tabela, os termos utilizados [9] são:
E1 – Módulo de Young na direção 1;
E2 – Módulo de Young na direção 2;
E3 – Módulo de Young na direção 3;
Gef – Combinação dos módulos Gij indicados entre parênteses [14];
G13 – Módulo de cisalhamento associado a deformações no plano 13;
G23 – Módulo de cisalhamento associado a deformações no plano 23;
G12 – Módulo de cisalhamento associado a deformações no plano 12.
Tabela 1 – Módulos elásticos determináveis pela Técnica de Excitação por Impulso de acordo com a orientação e em função dos modos de vibração.
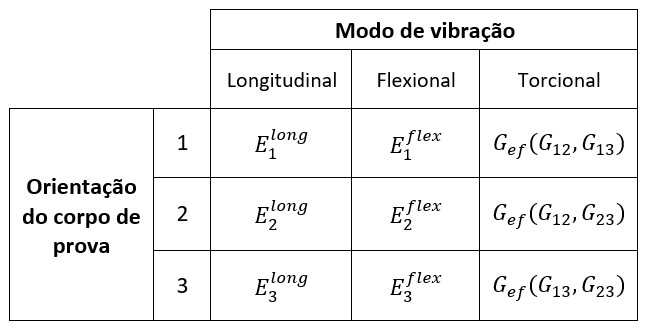
• Módulo de Young
- Pelo modo de vibração longitudinal
Quando o corpo de prova for solicitado na direção longitudinal (ver condições de contorno na Figura 6.c), o módulo elástico medido será na direção do comprimento do corpo de prova. Ou seja, a orientação da amostra é que determinará qual módulo está sendo determinado (E1, E2, E3 ou uma composição destes no caso de amostras cuja direção paralela ao seu comprimento não coincida a uma das orientações principais), como apresentado na Tabela 1.
- Modo de vibração flexional
Quando um material é flexionado, ocorrem solicitações simultâneas de tração e compressão, como ilustra a Figura 8 [10]. Para materiais homogêneos e isotrópicos, o módulo elástico obtido em um ensaio de flexão coincide com o módulo elástico medido na direção longitudinal. Portanto, o módulo elástico dinâmico obtido por meio do modo de vibração flexional é o mesmo que o obtido por meio do modo de vibração longitudinal [10]. Porém, sabe-se que, em flexão, a superfície do material é a região em que estão presentes os maiores valores de tensão normal. Por essa razão, caso a rigidez do corpo de prova seja diferente na superfície em comparação ao centro (por exemplo, se houver um gradiente de rigidez ao longo da espessura) ou caso a amostra apresente pequenos defeitos como poros, trincas e microtrincas em sua superfície, haverá uma discrepância nos valores obtidos pelo modo de vibração flexional e pelo modo longitudinal. Há diversos trabalhos focados na avaliação de madeiras que relatam diferenças de valores de acordo com o modo de vibração [8,11-13].
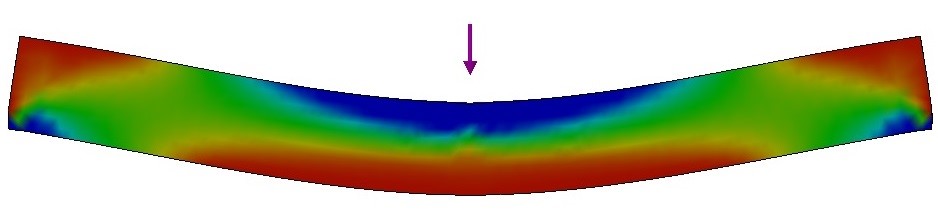
Figura 8 - Regiões em tração (vermelho) e em compressão (azul) durante um ensaio de flexão.
• Módulo de cisalhamento
- Modo de vibração torcional
Quando um corpo de prova é solicitado em torção, dois modos de cisalhamento agem simultaneamente no caso de materiais transversalmente isotrópicos e ortotrópicos. Se a torção ocorrer como descrito na Figura 6b, os módulos de cisalhamento atuantes serão os associados aos planos que estão sendo cisalhados (os quatro planos laterais do corpo de prova). Portanto, o módulo de cisalhamento calculado a partir da frequência de vibração torcional fundamental corresponderá a um módulo efetivo. Assim, o resultado obtido pelo Sonelastic® será uma combinação dos módulos de cisalhamento atuantes (a Tabela 1 indica os módulos de cisalhamento que compõem o valor efetivo para cada orientação) [14].
• Coeficiente de Poisson
A determinação do coeficiente de Poisson pela Técnica de Excitação por Impulso é indireta, sendo obtido a partir da correlação entre o módulo de Young e o módulo de cisalhamento do material, ou pelas equações recíprocas dos coeficientes de Poisson. Estas equações provêm da Teoria da Elasticidade e estão diretamente relacionadas às matrizes de rigidez e às simetrias, conforme apresentado a seguir:
- Material isotrópico:
- Material transversalmente isotrópico:
- Material ortotrópico:
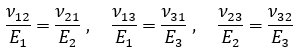
Onde: E é o módulo de Young, G o módulo de cisalhamento e ν o coeficiente de Poisson de um material isotrópico. O Apêndice B do Informativo técnico-científico ITC-06 apresenta a dedução destas equações, bem como explicações mais detalhadas sobre a medição do coeficiente de Poisson empregando a Técnica de Excitação por Impulso.
Simetria do material e os módulos obtidos empregando o Sonelastic®
Como já mencionado, os compósitos podem apresentar diferentes simetrias com relação às propriedades mecânicas. Sendo assim, faz-se necessário saber qual é a simetria, quais são os módulos elásticos que se deseja determinar e quais são as orientações existentes. A Tabela 2 apresenta um resumo das informações apresentadas e módulos mensuráveis empregando a Técnica de Excitação por Impulso com o Sonelastic®.
Tabela 2 – Módulos elásticos de acordo com a simetria, corpos de prova necessários e módulos elásticos possíveis de serem determinados com a Técnica de Excitação por Impulso (TEI).
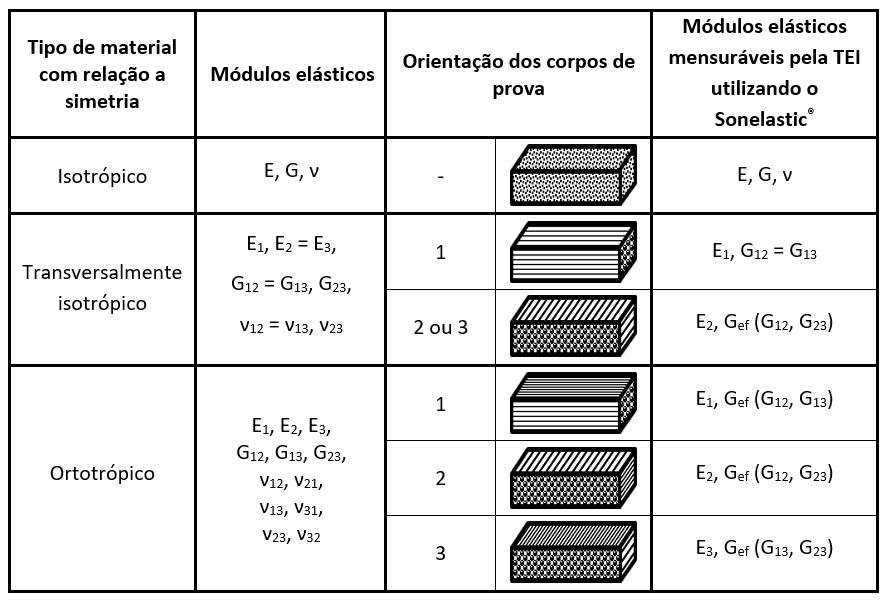
Para a determinação dos módulos elásticos de compósitos com a Técnica de Excitação por Impulso (TEI) é necessário preparar diferentes corpos de prova com orientações específicas conforme simetria do material. Vale ressaltar que é possível a caracterização de amostras que contenham fibras em ângulos intermediários (entre 0° e 90°), de modo que as propriedades medidas nessas direções estarão em concordância com a orientação do corpo de prova.
Considerações finais
Os compósitos, materiais formados pela combinação de dois ou mais materiais de naturezas distintas, podem ter seus módulos de elasticidade determinados de forma não-destrutiva pela Técnica de Excitação por Impulso, empregando-se as soluções Sonelastic®. Para tanto, é necessário conhecer a simetria do compósito e preparar corpos de prova de acordo com as direções do material.
Exemplos de clientes e aplicações na área de compósitos.
Referências bibliográficas
[1] ASTM International. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration. ASTM E1876-21, 2021.
[2] CHAWLA, K. K., Composite Materials: Science and Engineering. 3 ed. New York, Springer, 2012.
[3] Classificação dos materiais compósitos quanto ao tipo de reforço utilizado. Disponível em:
[4] DANIEL, I. M., ISHAI, O. Engineering Mechanics of Composite Materials. New York, Oxford University Press, 1994, 395 p.
[5] Vaso de pressão para gás natural fabricado pela 3M. Disponível em: < https://www.compositesworld.com/articles/the-markets-pressure-vessels-2012>. Acessado em 29 de Junho de 2022.
[6] Caracterização dos módulos elásticos de compósitos e de madeiras. Disponível em:
[7] Esquema de posicionamento e caracterização de acordo com a norma ASTM E1876. Disponível em: < https://www.sonelastic.com/pt/fundamentos/bases/modulos-elasticos.html> Acessado em: 06 de Julho de 2022.
[8] HEYLIGER, P., UGANDER, P., LEDBETTER, H. Anisotropic Elastic Constants: Measurement by Impact Resonance. Journal of Materials in Civil Engineering, pp. 356-363, set/out 2001.
[9] Adaptado de WANGAARD, F.F. The Mechanical Properties of Wood. New York: John Wiley & Sons, Inc, 1950.
[10] KAW, A.K. Mechanics of composite materials. 2 ed. Boca Raton, Taylor & Francis Group, 2006, 457 p.
[11] ROCHA, J.S., PAULA, E.V.C.M. de, SIQUEIRA, M.L. Flexão Estática em amostras pequenas livres de defeitos. Acta Amazonica, Manaus, p. 147-162. 1988.
[12] CHO, C.L., Comparison of Three Methods for Determining Young’s Modulus of Wood. Taiwan Journal for Science, pp. 297-306, Maio/2007.
[13] BUCUR, V., Acoustics of Wood. 2ª ed. Germany, Springer, 2006. p. 393.
[14] BODIG, J., JAYNE, B. A. Mechanics of wood and wood composites. Malabar (EUA), Krieger Publishing Company, 1993.
[15] GIBSON, R. F. Principles of composite material mechanics. USA, 1994, 425 p.
[16] CALLISTER Jr., W.D. Materials Science and Engineering. 7ª ed. New York: John Wiley & Sons, Inc, 2007.
[17] Curva Tensão-Deformação. Disponível em:
< http://www.ctb.com.pt/?page_id=1471>. Acessado em: 08 de Julho de 2014.
[18] NYE, J.F. Physical Properties of Crystals: their representation by tensors and matrices. Oxford: At the Clarendon Press. 1957.
[19] TSAI, S. W. Theory of Composites Design. Stanford: Stanford University, 2008, 230 p.
Saiba mais sobre os Sistemas Sonelastic® :
Sistema Sonelastic® para corpos de prova de pequeno porteSistema Sonelastic® para corpos de prova de médio porte
Sistema Sonelastic® para corpos de prova de grande porte
Sistema Sonelastic® customizado e orçamento


