Módulos elásticos e métodos de medição
Nesta página apresentamos uma visão geral dos módulos elásticos e dos principais métodos de medição. O intuito deste conteúdo é proporcionar para o Estudante, Engenheiro ou Pesquisador as informações básicas sobre o assunto visando facilitar a caracterização e a utilização destas propriedades, que são fundamentais para todas as classes de materiais e aplicações.
Os materiais, quando em serviço, são submetidos a cargas, por exemplo, a liga de alumínio em uma asa de avião, o aço em um eixo de um automóvel e o concreto em um pilar ou bloco de alvenaria. Nestas situações é necessário conhecer as características do material, dentre elas os módulos elásticos, para se projetar as peças e elementos de forma que as deformações resultantes sejam previsíveis e não excessivas ao ponto de ocorrer deformações plásticas, fadiga acelerada ou mesmo rupturas.

É necessário conhecer os módulos elásticos dos materiais para se projetar de forma que as deformações sejam previsíveis. Na imagem acima, o envergamento da régua é proporcional o módulo de elasticidade do metal - se o módulo fosse muito menor, a caneca teria caído.
O comportamento mecânico de um material depende em grande medida de sua resposta (ou deformação) à carga ou força a que é submetido. A propriedade que correlaciona a deformação elástica com a tensão é o módulo elástico, que tem diferentes definições dependendo do esforço aplicado. Além dos módulos elásticos, outras propriedades são igualmente importantes, por exemplo, a resistência mecânica e a ductilidade no caso de materiais metálicos. A aplicação de carga pode ser estática ou dinâmica.

Quanto maior o módulo de elasticidade, menor a deformação para uma dada tensão. Na imagem, dois blocos retangulares com as mesmas dimensões, um de borracha e o outro de alumínio, sendo prensados empilhados em uma morsa. O de borracha se deforma muito mais do que o de alumínio, visto que o módulo de elasticidade da borracha é em torno de 0,1 GPa enquanto o do alumínio é de 70 GPa.
A medição das propriedades mecânicas é realizada através de experimentos de laboratório cuidadosamente programados, de acordo com condições regidas por normas, por exemplo, pela ABNT NBR 8522 partes 1 e 2. No caso específico dos módulos elásticos, os métodos empregados podem ser dinâmicos, através de vibrações com diminutas amplitudes de deformação, ou estáticos, que submetem o corpo de prova a uma tensão conhecida e simultaneamente mensuram a deformação causada. Estes ensaios podem ser conduzidos tanto em temperatura ambiente como em função da temperatura, com ou sem atmosfera controlada.
O conhecimento dos módulos elásticos é alvo da atenção de produtores e consumidores de materiais, organizações de pesquisa e agências governamentais, que possuem necessidades e aplicações distintas. Consequentemente, é necessário que haja uma consistência na maneira segundo a qual os ensaios são conduzidos e na interpretação de seus resultados. Essa consistência é obtida mediante o uso de técnicas de ensaio padronizadas. O estabelecimento e a publicação das normas são coordenados por sociedades profissionais. No Brasil a ABNT (Associação Brasileira de Normas Técnicas) e nos Estados Unidos a ASTM (American Society for Testing and Materials) são responsáveis pelas normas de ensaios de materiais. Suas publicações são atualizadas a cada dois anos e uma série de normas está relacionada à determinação dos módulos elásticos, por exemplo, a ABNT NBR 8522 partes 1 e 2, que trata da medição do módulo de elasticidade do concreto.
Os materiais são selecionados para aplicações estruturais em função de combinações de características, como os módulos elásticos, a resistência mecânica, a durabilidade e os custos energéticos. O papel dos Engenheiros Estruturais é o de determinar as tensões e as distribuições destas tensões nos materiais. Este trabalho pode ser realizado mediante técnicas experimentais e/ou através de análises teóricas e computacionais das tensões, o que depende do conhecimento dos módulos elásticos. Engenheiros de Materiais e Engenheiros Metalúrgicos, por outro lado, estão preocupados com a produção e a fabricação de materiais para atender as exigências de serviços conforme previsto pelas análises de tensão. Isso envolve necessariamente uma compreensão das relações entre a microestrutura dos materiais e suas propriedades mecânicas, que estão diretamente correlacionadas com os módulos elásticos, permitindo que a caracterização destas propriedades seja utilizada para além do projeto, por exemplo, no controle de qualidade e tecnológico.
Definições
As soluções Sonelastic® se destinam a caracterização simultânea dos módulos elásticos e do amortecimento de materiais.
No caso de materiais isotrópicos, em que as propriedades não dependem da direção em que são medidas, os módulos elásticos são:
Módulo de Young ou módulo de elasticidade (Y ou E).É uma grandeza proporcional à rigidez do material quando este é submetido a tração ou compressão. Quando o comportamento é linear, o módulo de Young é igual a razão entre a tensão e a deformação específica do corpo, como mostrado na equação a seguir:
- E= Módulo de Young ou módulo de elasticidade (Pascal);
- σ= Tensão (Pascal);
- ε= Deformação específica (adimensional).
O módulo de cisalhamento, também conhecido como módulo de torção, é definido em função da tensão de cisalhamento e da deformação específica pela equação a seguir:
- G= Módulo de cisalhamento (Pascal);
- T= Tensão de cisalhamento (Pascal);
- Y= Deformação específica (adimensional).
A tensão de cisalhamento relaciona-se com uma força aplicada paralelamente a uma superfície com área A0, com o objetivo de causar o deslizamento de planos paralelos como ilustrado na figura a seguir. No caso, a deformação de cisalhamento, Υ, pode ser calculada pela tangente do ângulo θ.
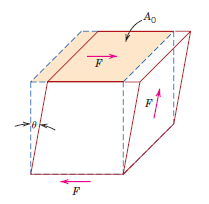
Representação da deformação por cisalhamento em um bloco retangular para o cálculo do módulo de cisalhamento (imagem da Wikipédia).
Mede a deformação em relação à direção de aplicação da carga de um material homogêneo e isotrópico. Em particular, no caso da razão de Poisson, a relação estabelecida não é entre tensão e deformação, mas sim entre deformações ortogonais pelas equações:
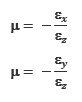
Em que:
- µ= Razão de Poisson (adimensional);
- εx= Deformação específica na direção x, que é transversal;
- εy= Deformação específica na direção y, que é transversal;
- εz= Deformação específica na direção z, que é na direção da carga;
- εx, εy e εz também são grandezas adimensionais.
O sinal negativo na equação da razão de Poisson é adotado porque as deformações transversais e no sentido da carga usualmente possuem sinais contrários. Materiais convencionais contraem-se transversalmente quando esticados e se expandem transversalmente quando comprimidos. A contração transversal em resposta à extensão devido a tração corresponde a um coeficiente de Poisson positivo. Ao se esticar uma borracha, por exemplo, você notará que ela se contrairá na direção transversal. Por outro lado, quando o material possui um coeficiente de Poisson negativo (casos especiais como o de metamateriais), ele se expande transversalmente quando tracionado. Materiais que apresentam coeficiente de Poisson negativo são denominados auxéticos.
Para materiais isotrópicos, o módulo de cisalhamento, o módulo de Young e a razão de Poisson estão correlacionados pela equação E=2G(1+µ). Para a maioria dos metais que possui razão de Poisson de 0,25, o módulo de cisalhamento G equivale a aproximadamente 40% do módulo de Young; desta forma, se o valor de um dos módulos for conhecido, o outro pode ser estimado.
Muitos materiais são anisotrópicos, isto é, as propriedades mecânicas variam a direção. Para esses materiais, as propriedades elásticas são completamente caracterizadas somente com a especificação de todas as constantes elásticas, sendo que o número destas depende da simetria do material. Veja o informativo Caracterização dos módulos de elasticidade de compósitos para mais detalhes. Observação: A maioria dos materiais policristalinos podem ser considerados isotrópicos, uma vez que a orientação dos grãos é aleatória.
Métodos de caracterização
As soluções Sonelastic® se destinam a caracterização simultânea dos módulos elásticos e do amortecimento de materiais.
Os módulos de elasticidade podem ser medidos pelas seguintes classes de métodos:
- Quase-estáticos (isotérmicos);
- Dinâmicos (adiabáticos).
Os métodos dinâmicos compreendem essencialmente os métodos pelas frequências naturais de vibração e pelo tempo de propagação de ondas ultrassônicas. Usualmente os métodos quase-estáticos são destrutivos, enquanto os métodos dinâmicos são não-destrutivos. Os valores determinados pelos métodos dinâmicos são maiores ou iguais àqueles determinados pelos métodos estáticos; a diferença é desprezível para materiais cerâmicos e metálicos, mas pode ser significativa para materiais viscoelásticos. No caso do concreto, é possível estimar o módulo de elasticidade estático tangente inicial (Eci) a partir do dinâmico (Ecd), conforme previsto no anexo B da norma ABNT NBR 8522-2:2021.
Métodos quase-estáticos
Os métodos quase-estáticos são baseados na análise da curva tensão-deformação. Tensão corresponde à força ou carga, por unidade de área, a que está sujeito o corpo de prova; deformação específica causada nas dimensões. O registro da tensão em função da deformação consiste na curva tensão-deformação. Nos ensaios estáticos, a carga é alterada lentamente em função do tempo e a deformação é medida e registrada para o cálculo do módulo, que pode ser o de Young ou de cisalhamento, dependendo de como a carga foi aplicada e a deformação medida. Para tal, há quatro maneiras principais segundo as quais uma carga pode ser aplicada: tracionando ou comprimindo o corpo de prova para a determinação do módulo de Young, e cisalhando ou torcendo para o módulo de cisalhamento; as mais comuns são a compressão e o tracionamento.
Métodos dinâmicos
Nos métodos dinâmicos os módulos elásticos são determinados a partir das frequências naturais de vibração (ressonâncias) do corpo de prova, ou a partir do tempo de propagação de ondas ultrassônicas. Os métodos dinâmicos permitem obter informações tanto quantitativas (módulos elásticos e velocidade do som), quanto qualitativas sobre a integridade (presença de trincas e defeitos). Como a carga dinâmica é muito baixa, o corpo de prova não é danificado com o ensaio dinâmico e pode ser empregado em sua função normalmente ou reensaiado outras vezes. A possibilidade de reensaiar o mesmo corpo de prova é interessante para estudos de degradação por eliminar a dispersão entre corpos de prova. Por exemplo, no estudo da resistência ao dano por choque térmico em refratários é possível avaliar a evolução do dano medindo-se o módulo de Young de forma intercalada com a aplicação de ciclos de choque térmico. Se fosse utilizado um método quase-estático, seria necessário um corpo de prova para cada medição.
Os métodos dinâmicos são normatizados e amplamente utilizados em todas as classes de materiais. No ano de 2021 foi publicada pela ABNT a norma NBR 8522-2 específica para a medição do módulo de elasticidade dinâmico de concreto e a NBR 8522-1 que prevê a estimativa do módulo de elasticidade estático tangente inicial do concreto (Eci) a partir do dinâmico (Ecd).
História dos métodos dinâmicos
O primeiro método dinâmico de aplicação prática foi desenvolvido por Förster em 1937. Neste método, uma barra de seção retangular do material a ser caracterizado é dependurada por dois fios, estando um deles conectado a um atuador e o outro a um sensor. As frequências de ressonância são determinadas com uma excitação senoidal de frequência variável associada à observação do pico de resposta da amostra, captado pelo sensor. Este método ainda é utilizado, principalmente para altas temperaturas.
Os fundamentos matemáticos para os cálculos dos módulos elásticos dinâmicos com precisão foram desenvolvidos entre a década de 1940 e 1960. Pickett apresentou em 1945 as equações para o cálculo dos módulos elásticos e da razão de Poisson a partir dos modos de vibração fundamentais. As equações propostas por Pickett contam com fatores de correção empíricos para barras e cilindros com baixa razão de aspecto. Em 1960 Kaneko apresentou um refinamento para as equações de Pickett generalizando-as para modos de vibração de qualquer ordem, e não apenas para os modos fundamentais.
Nas décadas de 1960 e 1970 foi desenvolvido o método de excitação por impulso e o equipamento Grindosonic; que popularizou a caracterização dos módulos elásticos dinâmicos e estendeu o método para o campo do controle de qualidade e inspeção. Neste método, a partir de determinadas condições de contorno mecânicas, o corpo de prova é excitado em um determinado modo de vibração por uma "pancada". O equipamento capta esta vibração com um sensor piezoelétrico ou microfone e informa ao usuário a respectiva frequência de ressonância, a partir da qual são calculados os módulos.
Nas décadas de 1990 e 2000 foram desenvolvidos sistemas de medição baseados em software para a caracterização dos módulos elásticos de materiais pela Técnica da Excitação por Impulso, com destaque para os Sistemas Sonelastic®.
Dada a importância, os procedimentos de caracterização não-destrutivos pelos métodos dinâmicos foram normatizados e realizados esforços interlaboratoriais para harmonização, além da elaboração de estudos e guias de boas práticas de caracterização.
Técnica de Excitação por impulso (Normas NBR 8522-2 e ASTM E1876) (Normas NBR 8522-2 e ASTM E1876)
Na Técnica de Excitação por Impulso é aplicado um impacto de curta duração no corpo de prova, que emite uma resposta acústica nas frequências naturais de vibração permitidas pelas condições de contorno mecânicas. A Figura a seguir mostra o posicionamento do corpo de um corpo de prova retangular para a medição da frequência de ressonância flexional. Nesta Técnica, o pulsador é o equipamento que aplica o impacto no corpo de prova e pode ser automático ou manual; o captador acústico detecta a resposta acústica e a transforma em sinal elétrico de maneira que possa ser processada pelo hardware e software do equipamento.
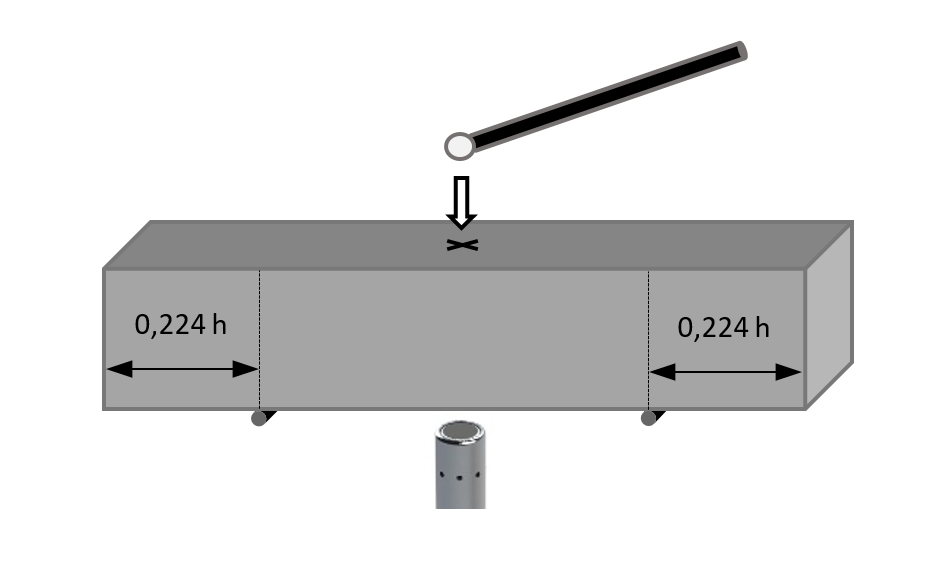
Condições de contorno mecânicas para o apoio e a excitação de barras retangulares para a determinação da frequência flexional fundamental pela Técnica de Excitação por Impulso.
Note que a amostra deve ser apoiada nas linhas nodais do modo flexional que ocorrem em 0,224L (L é o comprimento) e que o impulso é aplicado no centro onde a amplitude de vibração é máxima. Observação: A frequência flexional é proporcional a raiz quadrada do módulo de elasticidade. Na figura a seguir é mostrado um exemplo de corpo de prova de concreto no formato de barra retangular e o respectivo espectro de frequências após processamento pelo Software Sonelastic®.
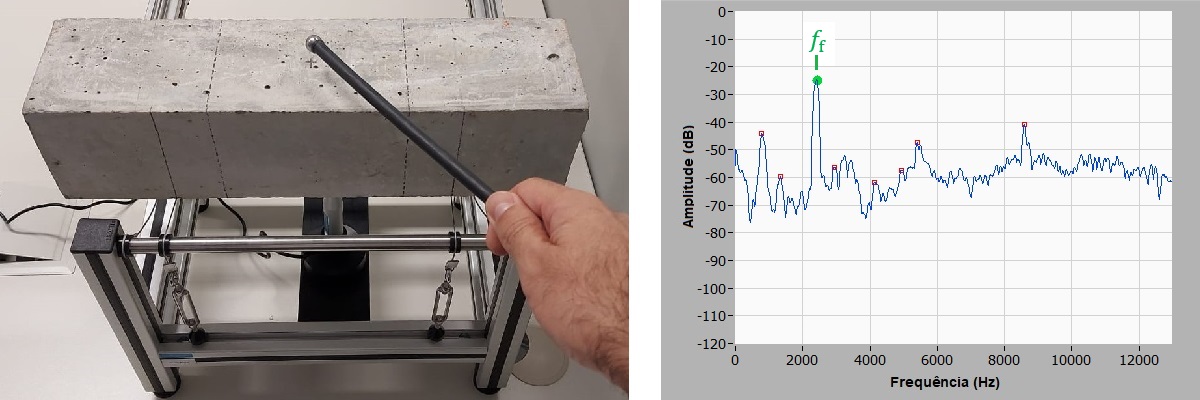
Exemplo de ensaio de uma barra retangular de concreto pela Técnica de Excitação por Impulso e o respectivo espectro de frequências após processamento pelo Software Sonelastic®.
Comparação entre os métodos
As soluções Sonelastic® se destinam a caracterização simultânea dos módulos elásticos e do amortecimento de materiais.
A tabela abaixo apresenta uma comparação entre as características dos principais métodos / equipamentos de medição do módulo de elasticidade aplicado a corpos de prova cilíndricos de concreto. Para outros materiais e geometrias os resultados podem ser diferentes.
| Métodos / Características | Quase-estático | Sonelastic® |
| Ensaio destrutivo? | Sim | Não |
| Incerteza típica: | 12% | 1,5% |
| Duração típica: | 1 hora | 6 minutos |
Segue abaixo algumas observações e notas importantes sobre as informações da tabela acima:
Incerteza típica:
A incerteza é metade da informação de qualquer medição. Em todos os métodos a incerteza será influenciada pelo acabamento e a precisão dimensional do corpo de prova, porém, a fonte principal de incerteza são as variáveis da medição. No método quase-estático, estas variáveis são a medição da tensão e da deformação específica, na Técnica de Excitação por Impulso, é determinação da frequência.
Referências bibliográficas das incertezas típicas:
- ABNT NBR 8522-1:2021, Concreto endurecido - Determinação dos módulos de elasticidade e de deformação - Parte 1: Módulo estáticos à compressão.
- ABNT NBR 8522-2:2021, Concreto endurecido - Determinação dos módulos de elasticidade e de deformação - Parte 2: Módulo de elasticidade dinâmico pelo método das frequências naturais de vibração.
Duração típica:
A duração típica corresponde ao tempo necessário para medir as dimensões, pesar e ensaiar os corpos de prova.
Referência bibliográfica da duração típica: THOMAZ, W. A. Estudo comparativo do módulo de elasticidade estático e dinâmico de concretos contendo agregados basálticos. Dissertação de Mestrado - UNILA. Foz do Iguaçu, 2020.



