Determinación de módulos elásticos de la madera y subproductos mediante la Técnica de Excitación por Impulso
El objetivo de esta página es presentar la teoría y metodología para la determinación no destructiva de los módulos elásticos de la madera y subproductos utilizando la Técnica de Excitación por Impulso. Se presenta una revisión bibliográfica y los avances en la aplicación de esta técnica, ya estandarizada para materiales isotrópicos [1], para la caracterización de maderas y subproductos.
Introducción
La madera, tanto por su disponibilidad como por sus características, fue uno de los primeros materiales utilizados por el hombre como medio estructural. Se puede clasificar como un compuesto orgánico sólido, formado principalmente por celulosa, cuya función principal es mantener el soporte de los árboles [2]. Es un material que proviene de tallos que crecen anualmente en diámetro y longitud. Además de la aplicación estructural, la madera también es útil como materia prima para subproductos como laminados encolados, madera contrachapada laminada, tableros de partículas y compuestos plásticos de madera (WPC).
![Figura 1: Puente sobre el río Montmorency, Bosque de Montmorency, Quebec, Canadá. Tiene un ancho de 44 m, una altura de 33 m y una anchura de 4,8 m [3].](/images/F1-ES-Puente-Madera-Rio-Montmorency-Canada-44m.jpg)
Figura 1: Puente sobre el río Montmorency, Bosque de Montmorency, Quebec, Canadá. Tiene un ancho de 44 m, una altura de 33 m y una anchura de 4,8 m [3].
Debido a las características microestructurales de su origen natural, las propiedades físicas de la madera dependen de la dirección de la carga [2]. Los tres ejes / direcciones principales de las maderas se ilustran en la Fig. 2 y se enumeran a continuación:
- Longitudinal (L): Eje paralelo a las fibras (dirección de las fibras);
- Radial (R): Eje normal a los anillos de crecimiento (perpendicular a las fibras en dirección radial);
- Tangential (T): Eje perpendicular a las fibras y tangente a los anillos de crecimiento.
![Figura 2 - Los tres ejes/direcciones principales de la madera con respecto a la dirección de la fibra y los anillos de crecimiento [4].](/images/F2-ES-Ejes-Direcciones-Principales-Madera-Direccion-Fibra-Anillos.png)
Figura 2 - Los tres ejes/direcciones principales de la madera con respecto a la dirección de la fibra y los anillos de crecimiento [4].
La madera se clasifica como un material ortótropo porque presenta planos de simetría ortogonales en los que las propiedades elásticas son constantes [5]. Esta clasificación es una aproximación, ya que dependiendo de la propiedad bajo análisis es posible verificar variaciones, por ejemplo, a lo largo de los anillos de crecimiento.
La determinación de los módulos elásticos es crucial para el desarrollo, selección y control de calidad de la madera y sus derivados, así como para simulaciones y cálculos estructurales. Estas aplicaciones son posibles debido a la sensibilidad de los módulos elásticos a la presencia de discontinuidades, defectos, grietas, nudos, cambios microestructurales y de composición química [6]. Una de las técnicas no destructivas que se ha vuelto popular para determinar el módulo de elasticidad es la Técnica de Excitación por Impulso, el foco de esta página.
Determinación de los módulos elásticos de la madera con el TEI
Fundamentos de la técnica
La Técnica de Excitación por Impulso determina los módulos elásticos de un material basándose en las frecuencias naturales de vibración de una muestra con geometría regular (barra o cilindro). Estas frecuencias son excitadas por un breve impulso mecánico, seguido de la adquisición de la respuesta acústica. Se realiza un análisis matemático de la respuesta acústica para obtener el espectro de frecuencias. Luego, los módulos elásticos dinámicos se calculan considerando la geometría, la masa, las dimensiones de la probeta y las frecuencias obtenidas por el análisis de la respuesta acústica [1].
Para la excitación y detección de modos de vibración determinados, es necesario establecer condiciones de contorno específicas. La figura 3 presenta un soporte de muestra con un dispositivo de impulso manual y un sensor acústico posicionado para excitar y detectar el modo de vibración en flexión.
![a) Montaje básico para caracterizar el modo de vibración flexional de una barra utilizando la Técnica de Excitación por Impulso [8]](/images/F3-A-ES-Montaje-modo-vibracion-flexural- barra-madera-TEI-Sonelastic.png)

Figura 3 - a) Montaje básico para caracterizar el modo de vibración flexional de una barra utilizando la Técnica de Excitación por Impulso [8] y b) Soporte SA-BC para barras y cilindros desarrollado y fabricado por ATCP Ingeniería Física.
El módulo de Young obtenido por la Técnica de Excitación por Impulso se denomina dinámico y es siempre mayor o igual al obtenido por un ensayo cuasiestático. No obstante, es posible establecer una correlación entre ellos [7].
Modos de vibración
Una muestra puede vibrar en diferentes modos y para cada modo hay una frecuencia fundamental específica. La Figura 4 presenta los principales modos fundamentales de vibración [9].
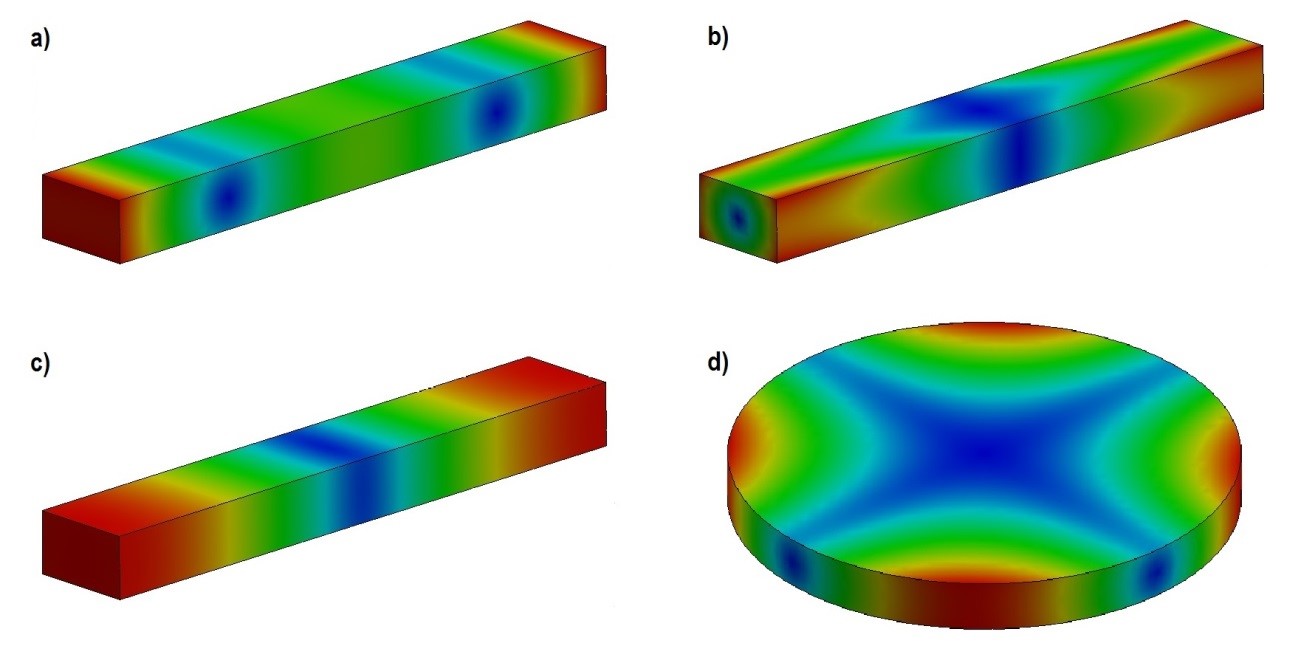
Figura 4 - Modos fundamentales de vibración: a) flexión, b) torsional, c) longitudinal y e) planar. La región azul representa el área de mínima amplitud de vibración, mientras que la roja representa el área de máxima amplitud.
Las condiciones de contorno impuestas a la muestra determinan qué modo de vibración se excitará. Las Figuras 5a-c [1,6] muestran las condiciones de contorno óptimas para los principales modos de vibración de una barra, mientras que la Figura 5d muestra las condiciones de contorno óptimas para un disco. Los módulos elásticos dinámicos correspondientes se calculan en función de las frecuencias resonantes de los modos de vibración excitados.
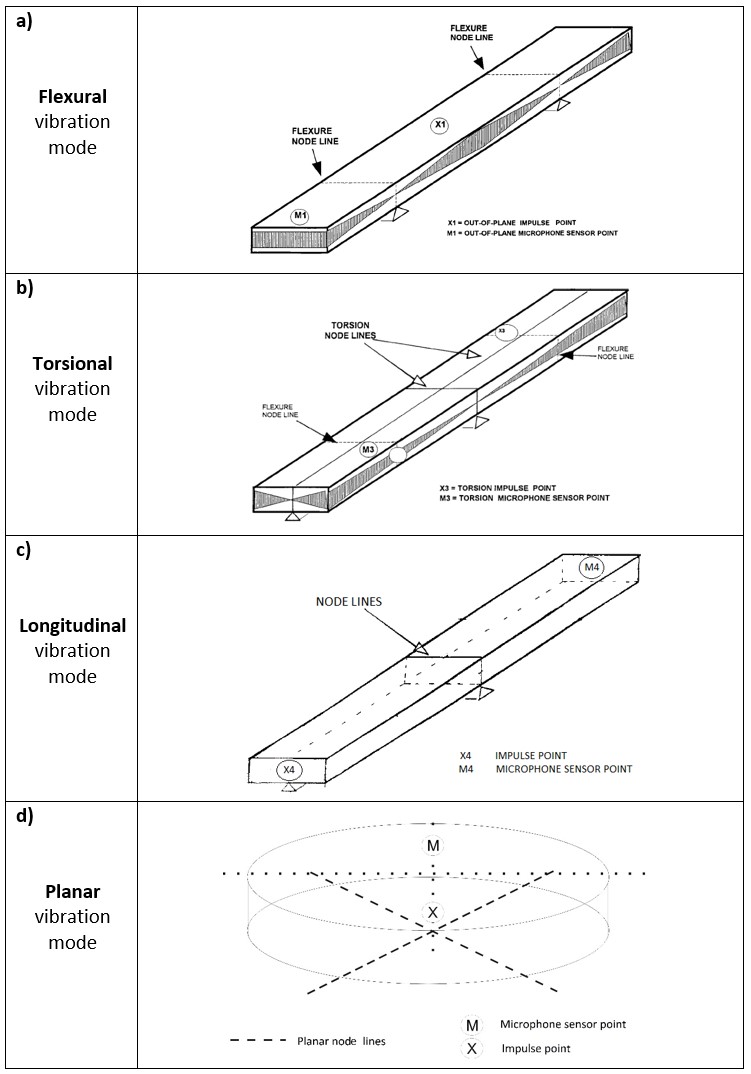
Figura 5 - Condiciones de contorno para la excitación de los modos de vibración fundamental (a) flexional, (b) torsional, (c) longitudinal y (d) planar.
Módulos elásticos de la madera
Las propiedades elásticas de la madera varían según la orientación de las fibras y de los anillos de crecimiento. Cuando se determinan utilizando la Técnica de Excitación por Impulso, es importante tener en cuenta la orientación para reportar los resultados correctamente. En el caso de los subproductos de la madera, el análisis es similar.
Tabla 1 - Módulos elásticos determinados por la Técnica de Excitación por Impulso en función de la orientación de las fibras y modos de vibración.
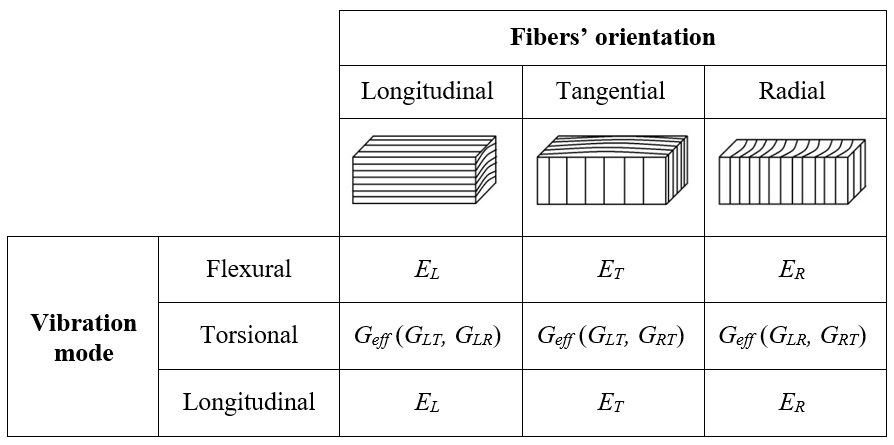
La Tabla 1 presenta los módulos elásticos de la madera que se pueden determinar usando la Técnica de Excitación por Impulso en dependencia de la orientación de las fibras y del modo de vibración. Los términos utilizados en la Tabla 1 se definen como [5,10]:
EL – Módulo de Young longitudinal;
ET – Módulo de Young tangencial;
ER – Módulo de Young radial;
Gef – Módulo de cortante efectivo determinado por el Sistema Sonelastic®, corresponde a una combinación de los módulos Gij mostrados entre paréntesis [5];
GLT – Módulo de Rigidez asociado al esfuerzo cortante en el plano LT resultante de los esfuerzos cortantes en los planos LR y RT;
GRT – Módulo de Rigidez asociado al esfuerzo cortante en el plano RT resultante de los esfuerzos cortantes en los planos LR y LT;
GLR – Módulo de rigidez asociado a la deformación por cortante en el plano LR resultante de los esfuerzos cortantes en los planos RT y LT.
• El módulo de Young
-Por modo de vibración longitudinal
Cuando la amuestra se excita en modo longitudinal (verifique las condiciones de contorno en la Figura 5c), el módulo de elasticidad obtenido se referirá a la orientación o eje paralelo a la longitud del espécimen. Por lo tanto, la orientación de la muestra determinará el módulo de elasticidad que se mide, como se presenta en la Tabla 1 (EL, ER, ET o una combinación de estas direcciones).
-Por modo de vibración de flexión
Cuando se flexiona una amuestra, hay tensión y compresión presentes como se muestra en la Fig. 6. Para materiales homogéneos e isotrópicos, el módulo elástico obtenido de una prueba de flexión coincide con el módulo elástico obtenido en una prueba axial (dirección longitudinal). De manera similar, el módulo elástico dinámico determinado por el modo de vibración de flexión es el mismo que por el modo de vibración longitudinal [11]. Sin embargo, al doblar, la superficie del espécimen está sujeta a esfuerzos mayores que su centro. Por ello, si una probeta presenta una rigidez de la superficie diferente a la del interior (por ejemplo, si hay un gradiente de rigidez a lo largo del espesor), o si la amuestra presenta pequeños defectos como poros, grietas y microfisuras en la superficie, habrá una diferencia entre los valores determinados por los modos de vibración flexional y longitudinal [10, 12-14].
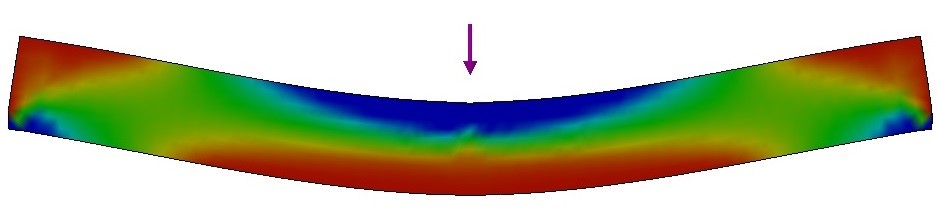
Figura 6 - Regiones bajo tensión (rojo) y bajo compresión (azul) durante un ensayo de flexión.
• Módulo de corte
-Por modo de vibración torsional
Cuando una muestra se somete a un ensayo de torsión, dos valores de módulos de corte actúan de manera concomitante sobre el material. Si hay torsión como la descrita en la Fig. 5b, los módulos de corte actuantes están asociados con las superficies cortadas (los cuatro laterales del espécimen). Por lo tanto, el módulo de cortante calculado utilizando la frecuencia de torsión fundamental corresponderá a un módulo efectivo. De esta forma, el resultado obtenido por el Sonelastic® será una combinación de los módulos de corte activos (en la Tabla 1 se indican los módulos de corte activos que componen el valor efectivo para cada orientación) [5].
• El coeficiente de Poisson
La Técnica de Excitación por Impulso no es adecuada para caracterizar el coeficiente de Poisson de materiales ortotrópicos como la madera. Sin embargo, con base en la Teoría de la Elasticidad y utilizando la matriz de rigidez, es posible obtener correlaciones entre los coeficientes de Poisson y los módulos elásticos. A continuación, encuentre estas relaciones:
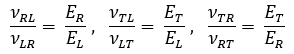
Para calcular los módulos elásticos, es necesario estimar lo coeficiente de Poisson. La Tabla 2 presenta una estimación e incertidumbre de acuerdo a los valores promedio que presenta las maderas típicas. Cabe mencionar que la sensibilidad del módulo de Young al error en la estimación de lo coeficiente de Poisson es baja.
Tabla 2 - Coeficiente de Poisson estimado y la respectiva incertidumbre para el cálculo del módulo de elasticidad de la madera en dependencia de la orientación de las fibras [5].
![Tabla 2 - Coeficiente de Poisson estimado y la respectiva incertidumbre para el cálculo del módulo de elasticidad de la madera en dependencia de la orientación de las fibras [5].](/images/T2-ES-Coeficiente-de Poisson-estimado-madera-orientacion-LT-LR-RT-RL-TR-TL.jpg)
• Parámetros derivados
A partir del módulo elástico y la densidad, es posible calcular el coeficiente de radiación sonora de la madera (R) y la impedancia acústica (z) [19]. El módulo de elasticidad a utilizar debe elegirse en función del modo de vibración.
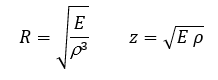
Valores esperados para madera blanda
La madera se puede clasificar en baja, media o alta densidad. La mayoría de las maderas de alta densidad tienen valores más altos de módulo elástico y resistencia [2]. La Tabla 3 presenta los valores de módulos elásticos previstos en función de EL para madera blanda, mostrando las propiedades elásticas de este tipo de madera de acuerdo con la variación de EL [5].
Tabla 3 - Parámetros elásticos previstos en función de EL para madera blanda (valores en GPa) [5].
![Tabla 3 - Parámetros elásticos previstos en función de EL para madera blanda (valores en GPa) [5].](/images/T3-ES-Parametros-elasticos-previstos-madera blanda-Er-El-Et-Glr-Glt-Grt.jpg)
El módulo de Young obtenido por la Técnica de Excitación por Impulso es dinámico y siempre mayor o igual que el obtenido por un ensayo cuasiestático. Sin embargo, es posible establecer una correlación entre los módulos estático y dinámico. A continuación, se muestra un ejemplo de correlación, en MPa, entre el módulo de Young determinado en la dirección longitudinal por ensayo cuasi-estático (ELE) y el módulo de Young dinámico determinado en la dirección longitudinal por Impulse Excitation Technique (ELD) [7]:

Ejemplo – Madera de eucalipto
Este ejemplo describe la determinación del módulo de elasticidad de una madera de Eucalipto (Eucalyptus spp) en dos orientaciones utilizando la Técnica de Excitación por Impulso y los Sistemas Sonelastic®.
Materiales y métodos
La Figura 7 muestra una vista superior de una sección de árbol, los círculos concéntricos corresponden a sus anillos de crecimiento. En esta figura, se ilustran tres posibles cortes de muestra. Los especímenes indicados por (1) y (2) presentan cortes ideales para obtener ET y ER, respectivamente. En (1), la dirección de la longitud es tangente a los anillos de crecimiento y en (2), la dirección de la longitud es paralela a la dirección de los anillos de crecimiento [5].
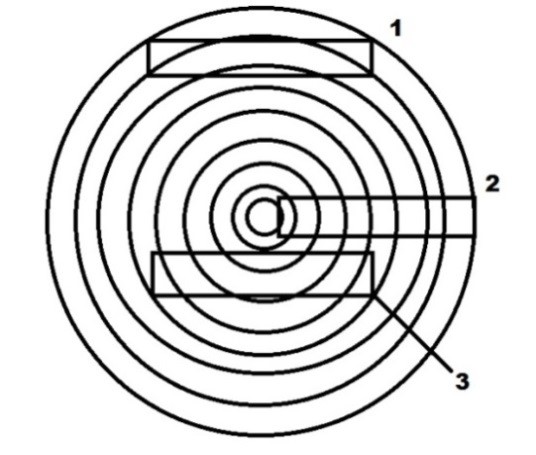
Figura 7 - Identificación de los mejores lugares para cortar las amuestras de madera para determinar ET (1) y ER (2). El corte presentado en (3) combina las direcciones R y T.
Si la muestra combina las direcciones R y T como se indica en (3), los valores obtenidos serán efectivos y resultarán de una combinación entre ER y ET.
Las Figuras 8 y 9 indican la orientación de las fibras de las muestras de madera ensayadas. El espécimen de la Fig. 8 presenta sus fibras alineadas paralelas a su longitud (estas barras fueron indicadas por el índice “L”). El espécimen de la Fig. 9 tiene sus fibras orientadas transversalmente y hay una combinación entre la dirección radial y tangencial a lo largo de su longitud (estas barras se indicaron con el índice "RT").

Figura 8 - Muestra con fibras en la dirección longitudinal (L).

Figura 9 - Muestra con fibras en las direcciones radial y tangencial (RT).
Las probetas fueron ensayadas con respecto a los principales modos de vibración (flexión, torsión y longitudinal) utilizando el soporte ajustable para barras y cilindros SA-BC, el Dispositivo Automático de Impulso Electromagnético IED, el sensor acústico direccional CA-DP y el Sonelastic Software® (estos elementos forman parte del Sistema Sonelastic® para probetas de tamaño mediano que se muestra en la Fig. 10).
Se adoptó una relación de Poisson de 0,25 ± 0,25 para calcular los módulos elásticos. Como se mencionó anteriormente, este valor puede variar significativamente según la orientación de las fibras. Por esta razón, se consideró una incertidumbre de 0,25 para incluir todos los valores posibles de esta propiedad. Nota: La influencia del coeficiente de Poisson en el cálculo de los módulos elásticos es baja, esto se puede verificar comprobando las incertidumbres presentadas en las Tablas 4 y 5.

Figura 10 - Equipo Sonelastic® desarrollado por ATCP Ingeniería Física para determinación de los módulos elásticos por la Técnica de Excitación por Impulso.
Resultados y discusiones
Las muestras se organizaron en dos grupos según la dirección de la fibra. Las tablas 4 y 5 muestran los módulos elásticos determinados en cada modo de vibración.
Tabla 4 - Módulos elásticos obtenidos en función del modo de vibración (muestras "RT").
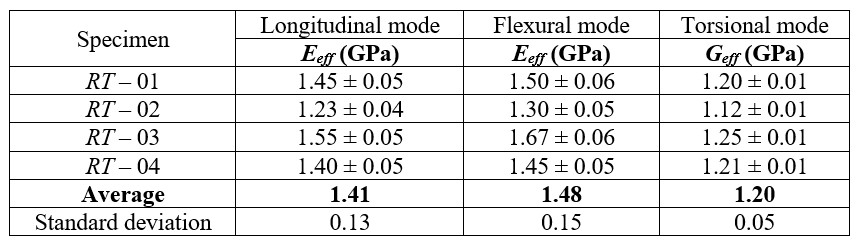
Tabla 5 - Módulos elásticos obtenidos en función del modo de vibración (muestras "L").
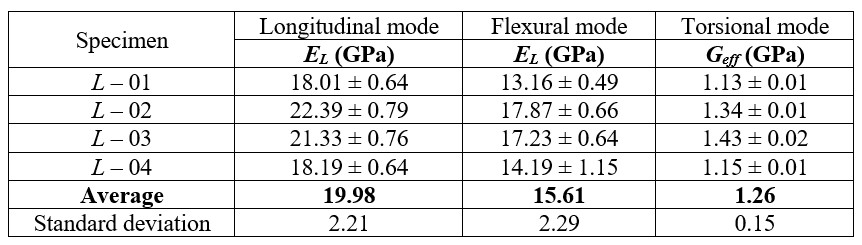
Los módulos de Young en la Tabla 4 son efectivos porque las muestras presentan una combinación entre las direcciones R y T alineadas paralelas a sus longitudes. Los valores medidos para muestras "L" están representados por EL porqué las fibras son paralelas a la longitud (Tabla 5).
Existe una diferencia entre los valores de los módulos elásticos obtenidos en los modos de vibración longitudinal y en flexión, principalmente para las probetas “L”. Esta diferencia se debe a la presencia de defectos superficiales, que influyen más en los resultados en el modo de vibración por flexión; también puede existir un gradiente de rigidez a lo largo del espesor, de manera que la superficie sea más o menos rígida que su interior, influyendo en los resultados. Para la madera, existe una tendencia a que las propiedades obtenidas con el modo de vibración longitudinal sean superiores a las obtenidas en el modo en flexión. [10,12-14].
Finalmente, Geff consiste en un módulo de corte efectivo, que es una combinación de los módulos relacionados con los planos que se cortan en la vibración torsional. Por ejemplo, el valor de Geff para las muestras “L” es una combinación entre GLR y GLT. Para probetas “RT”, este análisis es aún más complejo porque la dirección de la longitud de la probeta no corresponde a una orientación definida (L, R o T).
Consideraciones finales
La madera y los sus subproductos son materiales anisotrópicos y sus módulos elásticos dependen de la orientación de las fibras y del modo de vibración cuando se prueban mediante la Técnica de Excitación por Impulso.
A partir de la orientación de la muestra y de las condiciones de contorno para los modos de vibración flexional y longitudinal, es posible obtener los principales módulos elásticos de la madera: EL, ER y ET. La Técnica de Excitación por Impulso también permite la caracterización de módulos de corte efectivos por modo de vibración torsional.
Ejemplos de clientes y aplicaciones en el área de composites, madera y derivados.
Referencias
[1] ASTM International. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM E 1876. 2007. 15 p.
[2] DİNÇKAL, Ç. Analysis of Elastic Anisotropy of Wood Material for Engineering Applications. Journal of Innovative Research in Engineering and Science, Global Research Publishing, pp. 67-80, abr. 2011.
[3] Ponte de Madeira na floresta de Montmorency. Disponível em:
[4] Adaptado de CALIL JUNIOR, C.; LAHR, F.A.R.; DIAS, A.A. Dimensionamento de elementos estruturais de madeira. Barueri: Manole, 2003. 152 p.
[5] BODIG, J., JAYNE, B. A. Mechanics of wood and wood composites. Malabar (EUA), Krieger Publishing Company, 1993.
[6] COSSOLINO, L.C., PEREIRA, A.H.A. Módulos elásticos: visão geral e métodos de caracterização. Informativo Técnico – ATCP Engenharia Física. Out/2010. Disponível em:
[7] SEGUNDINHO, P.G.A., COSSOLINO, L.C., PEREIRA, A.H.A, JUNIOR, C.C. Aplicação do método de ensaio das frequências naturais de vibração para obtenção do módulo de elasticidade de peças estruturais de madeira. Revista Árvore, Viçosa-MG, v.36, n.6, p.1155-1161, 2012.
[8] Esquema de posicionamento e caracterização de acordo com a norma ASTM E1876. Disponível em:
[9] HEYLIGER, P., UGANDER, P., LEDBETTER, H. Anisotropic Elastic Constants: Measurement by Impact Resonance. Journal of Materials in Civil Engineering, pp. 356-363, set/out 2001.
[10] WANGAARD, F.F. The Mechanical Properties of Wood. New York: John Wiley & Sons, Inc, 1950.
[11] KAW, A.K. Mechanics of composite materials. Boca Raton: Taylor & Francis Group, 2 ed, 2006, 457 p.
[12] ROCHA, J.S., PAULA, E.V.C.M. de, SIQUEIRA, M.L. Flexão Estática em amostras pequenas livres de defeitos. Acta Amazonica, Manaus, p. 147-162. 1988.
[13] CHO, C.L., Comparison of Three Methods for Determining Young’s Modulus of Wood. Taiwan Journal for Science, pp. 297-306, Maio/2007.
[14] BUCUR, V., Acoustics of Wood. 2ª ed. Germany: Springer, 2006. p. 393.
[15] WANGAARD, F. F. The Mechanical Properties of Wood. John Wiley & Sons, Inc., New York, 1950.
[16] CALLISTER Jr., W.D. Materials Science and Engineering. 7ª ed. New York: John Wiley & Sons, Inc, 2007.
[17] Curva Tensão-Deformação. Disponível em:
< http://www.ctb.com.pt/?page_id=1471>. Acessado em: 08 de Julho de 2014.
[18] NYE, J.F. Physical Properties of Crystals: their representation by tensors and matrices. Oxford: At the Clarendon Press. 1957.
[19] Ulrike G.K. Wegst, Wood for sound. American Journal of Botany 93(10):1439-1448. October 2006.
Descubra los Sistemas Sonelastic® :
Sistemas Sonelastic® para muestras pequeñasSistemas Sonelastic® para muestras medianas
Sistemas Sonelastic® para muestras grandes
Cotación para Sistema Sonelastic® personalizado


